Cho a > 0 và a khác 1 . Tìm mệnh đề đúng trong các mệnh đề sau
A. log a ( x y ) = l og a x . log a y ( ∀ x , y ∈ R )
B. log a x n = n log a x ( ∀ n > 0 . n ≠ 0 )
C. log a x c ó n g h ĩ a ∀ x ∈ R
D. log a 1 = a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

Đáp án D
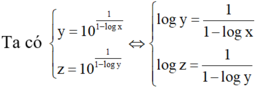
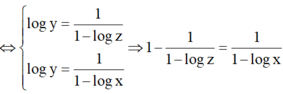
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .

Đáp án B
Diện tích tam giác A B C : S A B C = 1 2 . A B . A C . sin A ^ = 3 a 2 4
Có B C = A B 2 + A C 2 − 2. A B . A C . c o s B A C ^ = a 3
Ta có A B ' = a 2 + a 2 = a 2 , A I = a 2 + a 2 2 = a 5 2
Ta được A B ' 2 + A I 2 = 2 a 2 + a 5 2 2 = 13 a 2 4 = B ' I 2 . Suy ra tam giác AB’I vuông tại A, có diện tích bằng: S A B I = 1 2 . A B ' . A I = 1 2 a 2 . a 5 2 = a 2 10 4
Tam giác ABC là hình chiếu vuông góc của tam giác AB’I trên A B C nên ta có:
S A B C = c o s α . S A B ' I ⇔ c o s α = a 2 3 4 : a 2 10 4 = 30 10
Chú ý: Nếu không được “may mắn có Δ A B ' I vuông”, ta có thể sử dụng công thức He-rông để tính diện tích tam giác A B ' I

Chọn đáp án C
Mệnh đề 1 và mệnh đề 3 đúng.
Mệnh đề 2 sai tại điều kiện x > y > 0 , sửa lại:
Nếu x > 0 , y > 0 và 0 < a ≠ 1 thì mệnh đề
![]()