Bài này ko xuất hiện số 0 nên tính toán nhẹ được 1 nửa

Lập được \(P_5^3=60\) số

Do vai trò của các chữ số là như nhau, nên số lần xuất hiện của mỗi chữ số ở mỗi hàng (trăm, chục, đơn vị) là như nhau. Có 60 số và 5 chữ số, vì thế, ở mỗi hàng mỗi chữ số sẽ xuất hiện \(60:5=12\) lần (ví dụ như số 2 sẽ xuất hiện ở hàng đơn vị tổng cộng 12 lần, ở hàng trăm cũng 12 lần...)

Do đó tổng giá trị các chữ số ở hàng đơn vị là:

 \(12.1+12.2+12.3+12.4+12.6=12\left(1+2+3+4+6\right)=192\)

Ở hàng chục, giá trị của 1 chữ số gấp 10 lần hàng đơn vị (ví dụ số 32 thì số 2 chỉ có giá trị là 2, nhưng ở số 23 thì số 2 có giá trị là 20), do đó, tổng giá trị các chữ số ở hàng chục là:

\(10.\left(12.1+12.2+12.3+12.4+12.6\right)=10.12\left(1+2+3+4+6\right)\)

Tương tự, tổng giá trị ở hàng trăm là: 

\(100.12.\left(1+2+3+4+6\right)\)

Tổng các chữ số lập được là:

\(\left(1+10+100\right).12.\left(1+2+3+4+6\right)=21312\)

Tổng quát: cho n chữ số 1,2,... (ko xuất hiện chữ số 0), lập các số tự nhiên có m<n chữ số khác nhau, vậy tổng lập được là:

\(\underbrace{11...1}_{\text{m chữ số 1}}\times\dfrac{P_n^m}{n}\times(1+2+...)\)

Đáp án B.

Chọn 3 chữ số trong 5 chữ số có C 5 3   =   10  cách.

Và sắp xếp 3 chữ số ở trên theo thứ tự có 3! = 6 cách.

Suy ra có 6.10 = 60 số có 3 chữ số đôi một khác nhau.

Tổng các chữ số 1, 2, 3, 4, 6 là 16 và gọi số cần tìm có dạng  a b c

Khi đó, mỗi chữ số 1, 2, 3, 4, 6 sẽ xuất hiện ở 3 vị trí a,b,c tương ứng là 12 lần.

Vậy tổng của các số lập được là 12.16.(10²+10¹+10⁰) = 21312

Đáp án B nha :3

Chọn B

Số phần tử của tập hợp E là 

Vì 

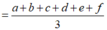
Mà  chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại  ra một số chia hết cho 3. Ta có 3 trường hợp sau:

1) Trường hợp 1:

Loại bỏ số 0, khi đó a + b = c + d = e + f = 7

Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.

Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.

Trường hợp này có 48 số.

2) Trường hợp 2:

Loại bỏ số 3, khi đó a + b = c + d = e + f = 6

Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.

Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d  có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.

Trường hợp này có 40 số.

3) Trường hợp 3:

Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.

Vậy trong tập hợp E có tất cả 48 +  40 + 40 = 128 số có dạng a b c d e f ¯  sao cho  a + b = c + d = e + f

Xác suất cần tìm là: 

Các số là:

2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320

2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563

Quá trời luôn. Bạn đánh siêu thật !

1.

Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)

Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách

Tổng cộng: \(4.A_6^4\) cách

2.

Gọi chữ số cần lập có dạng \(\overline{abcd}\)

a.

Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách

Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách

\(\Rightarrow A_6^4-A_5^3=300\) số

b.

Để số được lập là số chẵn \(\Rightarrow\) d chẵn

TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn

TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)

a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn

\(\Rightarrow2.4.4.3=96\) số

Tổng cộng: \(A_5^3+96=156\) số

Xác suất \(P=\dfrac{156}{300}=...\)

cho e hỏi chữ "A" bấm máy sao

Đáp án B

Gọi số cần lập là a b c d ¯  

TH1: d = 0 suy ra có 5.4.3 = 60 số

TH2: d   =   2 ;   4  suy ra có 2.4.4.3 = 96 số

Theo quy tắc cộng có: 60 + 96 = 156 số

a: \(\overline{abc}\)

a có 3 cáhc

b có 4 cáhc

c có 4 cách

=>Có 3*4*4=48 cách

b: \(\overline{abcd}\)

a có 3 cách

b có 3 cách

c có 2 cách

d có 1 cách

=>Có 3*3*2=18 cách

c: \(\overline{abc}\)

c có 1 cách

a có 3 cách

b có 4 cách

=>Có 1*3*4=12 cách

d: \(\overline{abcd}\)

TH1: d=0

=>Có 3*4*4=48 cách

TH2: d<>0

d có 2 cách

a có 3 cách

b có 4 cách

c có 4 cách

=>Có 4*4*3*2=16*6=96 cách

=>Có 144 cách

Cảm ơn bạn nhiều!