Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh SA vuông góc với đáy và cạnh AC=2a. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 30°. Thể tích khối chóp S.ABCD là
A. a 3 3 6
B. 2 a 3 6 9
C. 2 a 3 6 3
D. a 3 6 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
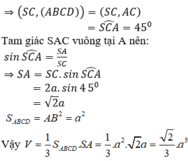

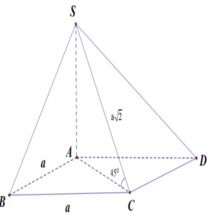
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
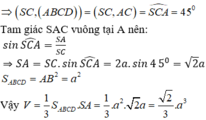

Đáp án D
Vì S A ⊥ ( A B C D ) B C ⊥ A B ⇒ B C ⊥ ( S A B ) ⇒ S B C ; A B C D ^ = S B A ^
Tam giác SAB vuông tại A, có tan S B A ^ = S A A B ⇒ S A = 2 a . tan 30 ° = 2 a 3
Thể tích khối chóp S.ABCD là
V
=
1
3
S
A
.
S
A
B
C
D
=
1
3
2
a
3
4
a
2
=
8
a
3
2
9
Vậy tỉ số
3
V
a
3
=
24
a
3
3
9
:
a
3
=
8
3
3

Chọn A.
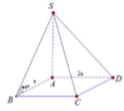
Ta có: ![]()
![]() Do tam giác SAB vuông cân tại A nên SA = AB = a.
Do tam giác SAB vuông cân tại A nên SA = AB = a.
Vậy ![]()