Cho hình chữ nhật có diện tích 20 (đơn vị diện tích) và hai kích thước x và y (đơn vị dài). Theo bảng vừa thành lập, hãy biểu diễn bảy điểm của đồ thị hàm số y = 20/x trên mặt phẳng tọa độ xOy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2018
Điểm thuộc đồ thị có y = 6 thì ứng với x = 2 .
Vậy khi diện tích hình chữ nhật bằng 6(m2) thì cạnh x = 2 (m)
Điểm thuộc đồ thị có y = 9 thì ứng với x = 3.
Vậy khi diện tích hình chữ nhật bằng 9 (m2) thì cạnh x = 3 (m)
CM
22 tháng 2 2018
- Công thức biểu diễn diện tích y theo x là y = 3x
- Vì với mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số đại lượng x
- Vẽ đồ thị hàm số :
+ Chọn 1 điểm khác O thuộc đồ thị : chọn x = 1 được y = 3 ⇒ A(1 ;3) thuộc đồ thị.
+ Đường thằng OA là đồ thị hàm số y = 3x
Vẽ đồ thị:
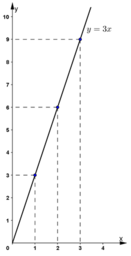
Trên đồ thị thấy :
+ Điềm thuộc đồ thị có x = 3 thì ứng với y = 9
Vậy khi x = 3 m thì diện tích hình chữ nhật bằng 9(m2)
+ Điểm thuộc đồ thị có x = 4 thì ứng với y = 12
Vậy khi x = 4 m thì diện tích hình chữ nhật bằng 12 (m2)
CM
4 tháng 3 2018
Đáp án A.
Đơn vị dài là 2 cm vậy nên đơn vị diện tích quy đổi ra sẽ là 2 2 = 4 c m .
Khi đó S = − 1 2 x 3 d x .4 = 15 c m 2
CM
22 tháng 1 2018
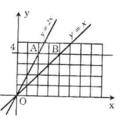
a) Vẽ đồ thị:
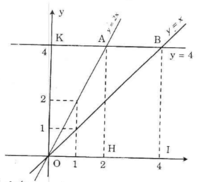
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
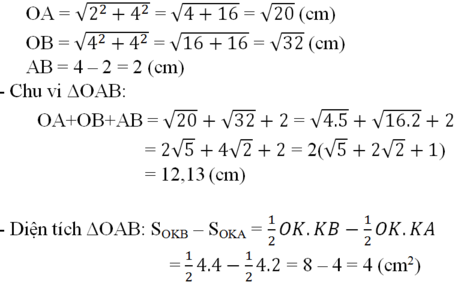
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)
CM
19 tháng 11 2019
a) - Với hàm số y = x + 1:
Cho x = 0 => y = 1 ta được M(0; 1).
Cho y = 0 => x + 1 = 0 => x = -1 ta được B(-1; 0).
Nối MB ta được đồ thị hàm số y = x + 1.
- Với hàm số y = -x + 3:
Cho x = 0 => y = 3 ta được E(0; 3).
Cho y = 0 => -x + 3 = 0 => x = 3 ta được A(3; 0).
Nối EA ta được đồ thị hàm số y = -x + 3.
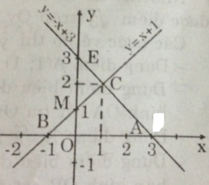
b) Từ hình vẽ ta có:
- Đường thẳng y = x + 1 cắt Ox tại B(-1; 0).
- Đường thẳng y = -x + 3 cắt Ox tại A(3; 0).
- Hoành độ giao điểm C của 2 đồ thị hàm số y = x + 1 và y = -x + 3 là nghiệm phương trình:
x + 1 = -x + 3
=> x = 1 => y = 2
=> Tọa độ C(1; 2)
c) Ta có: AB = 3 + 1 = 4
CM
10 tháng 2 2017
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
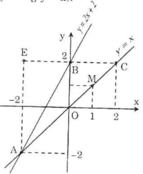
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
HH
2 tháng 2 2021
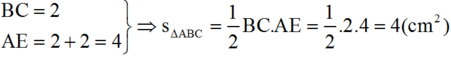
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)
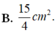
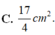
Vẽ hình