Biết rằng mức lương của một kỹ sư ở công ty X trong quý I năm 2017 (3 tháng đầu tiên của năm 2017) là S 0 (triệu đồng), kể từ quý II mức lương sẽ được tăng thêm 0,5 triệu đồng mỗi quý. Tổng lương của kỹ sư đó tính từ quý I năm 2017 đến hết quý IV năm 2022 là 1002 (triệu đồng). Tính tổng lương S (triệu đồng) của kỹ sư tính từ quý I năm 2017 đến hết quý IV năm 2015.
A. S = 1611
B. S = 342
C. S = 324
D. S = 1911



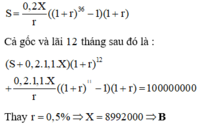

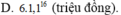
Đáp án A
Từ quý I năm 2017 đến hết quý IV năm 2022 là 24 quý.
Tổng lương chính là tổng của cấp ố cộng với