Trong các hình chữ nhật có chu vi bằng 300m, hình chữ nhật có diện tích lớn nhất bằng
A. 22500 m 2
B. 900 m 2
C. 5625 m 2
D. 1200 m 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x(m) là cạnh thửa ruộng hình vuông
y(m) là chiều dài thửa ruộng hình chữ nhật
ĐK: x,y>0
Chu vi hình vuông là : 4x (m)
Chu vi hình chữ nhật là : (x+y).2 (m)
Theo đề ta có phương trình : (x+y).2-4x=30
<=>-2x+2y=30(1)
Diện tích hình vuông là : x2(m2)
Diện tích hình chữ nhật là: xy (m2)
Theo đề ta có phương trình xy-x2=300(2)
Từ (1) và (2) ta có HPT: \(\begin{cases}-2x+2y=30\\xy-x^2=300\end{cases}\)
Giải HPT ta được: x=20;y=35
Diện tích thửa ruộng hình vuông là: 202=400 (m2)
Diện tích thửa ruộng hình chữ nhật là: 20.35=700 (m2)
Theo đề bài, ta có: (C = R)
Chcn = (D + R) x 2 = 2D + 2R
Chv = C x 4 = 4C
Chcn - Chv = 2D + 2R - 4C
30m = 2D - 2C
Ta thấy, chu vi hình vuông nhỏ hơn chu vi hình chữ nhật chính là 2 lần chiều dài hơn 2 lần chiều rộng (2 lần cạnh hình vuông). Vậy, chiều dài hơn chiều rộng là:
30 : 2 = 15 (m)
Ta có: (C = R)
Shcn = D x R
Shv = C x C
Shcn - Shv = D x R - C x C
300m2 = C(D - R)
300m2 = C x 15
Vậy, chiều rộng hình chữ nhật (cạnh hình vuông) là:
300 : 15 = 20 (m)
Chiều dài của hình chữ nhật là:
20 + 15 = 35 (m)
Diện tích của thửa ruộng hình chữ nhật là:
35 x 20 = 700 (m2)
Diện tích của thửa ruộng hình vuông là:
20 x 20 = 400 (m2)
Đáp số: Diện tích thửa ruộng hình chữ nhật là 700m2
Diện tích thửa ruộng hình vuông là 400m2

a) Dài: 3x
Rộng x
=> S: 3x.x=3x2=27
<=>x.x=9
<=>x=3
=> Rộng : 3(cm) ; Dài: 9 (cm)
=> Chu vi: (3+9) x 2=24(cm)
b) Trong các hình chữ nhật cùng chu vi thì hình vuông có diện tích lớn nhất.

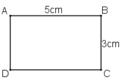
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2)
Hình chữ nhật có kích thước là 1cm x 12cm có diện tích là 12cm2 và chu vi là (1 + 12).2 = 26 (cm) (có 26 > 15)
Hình chữ nhật kích thước 2cm x 7cm có diện tích là 14cm2 và chu vi là (2 + 7).2 = 18 (cm)
(có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
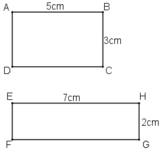
b) + Chu vi hình chữ nhật ABCD đã cho là (5 + 3).2 = 16 cm
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là: 16 : 4 = 4 cm
Diện tích hình vuông này là 4.4 = 16 cm2
(Ở trên hình là ví dụ hình vuông MNPQ có cạnh là 4cm)
Vậy SHCN < SHV
+ Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Gọi cạnh của hình chữ nhật có độ dài lần lượt là a, b.
Hình vuông có cùng chu vi với hình chữ nhật nên cạnh hình vuông là 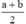
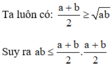
⇒ Hình vuông có diện tích lớn nhất.

Đáp án C
Gọi a,b là chiều dài và chiều rộng của hình chữ nhật. Ta có:
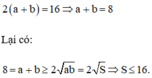
Đáp án là C
Giả sử hình chữ nhật có chiều dài và chiều rộng lần lượt là a, b(0<a, b<150), đơn vị: m.
Từ giả thiết, ta có a+b=150
Diện tích hình chữ nhật là S=a.b
Cách 1:
Áp dụng bất đẳng thức Cô – si, ta có
a b ≤ a + b 2 ⇔ a b ≤ 75 ⇔ a b = 5625 ⇔ S = 5625
Dấu bằng xảy ra a = b a + b = 150 ⇔ a = 75 b = 75
Hay max S= 5625 m 2
Cách 2:
Ta có a+b=150 <=> b=150-a
Khi đó S=a.b=a(150-a)= - a 2 + 150 a
Xét hàm số f a = - a 2 + 150 a 0 < a < 150
f ' a = - 2 a + 150 , f ' a = 0 ⇔ a = 75
Vậy max S= 5625 m 2