cho 4 đường thẳng a;b;c;d phân biệt. Số giao điểm của các đường thẳng trên bằng bao nhiêu? (Mỗi trường hợp chỉ cần vẽ 1 hình)
Ai làm nhanh và đúng nhất mình sẽ tick
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì a//b và b⊥c nên a⊥c
b, Ta có \(\widehat{D_2}=\widehat{D_4}=65^0\) (đối đỉnh)
Vì a//b nên \(\widehat{C_4}=\widehat{D_2}=65^0\) (so le trong)
\(\widehat{C_3}+\widehat{C_4}=180^0\) (kề bù)
Hay \(\widehat{C_3}=180^0-65^0=115^0\)

Để vẽ được các đường thẳng như yêu cầu, chúng ta có thể sử dụng nguyên tắc "mỗi đường thẳng đi qua 2 trong 4 điểm trên".
a. Để vẽ 6 đường thẳng, ta có thể chọn 2 điểm từ 4 điểm trên và vẽ đường thẳng đi qua chúng. Vì có 4 điểm, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 6 đường thẳng.
b. Tương tự, để vẽ 4 đường thẳng, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 4 đường thẳng.
c. Để vẽ 2 đường thẳng, ta cũng có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 2 đường thẳng.
Với các yêu cầu trên, chúng ta có thể vẽ được số đường thẳng tương ứng.

a. Đường thẳng đi qua gốc tọa độ khi tung độ gốc bằng 0
\(\Rightarrow a=0\)
b. Đường thẳng song song với \(y=\left(\sqrt{3}+1\right)x+4\) khi:
\(\left\{{}\begin{matrix}a+1=\sqrt{3}+1\\a\ne4\end{matrix}\right.\) \(\Rightarrow a=\sqrt{3}\)

+1 đường thì 4 điểm đó thẳng hàng
+4 đường thì có 3 điểm thẳng hàng
+6 đường thì không có 3 điểm nào thẳng hàng
ĐÚNG ĐẤY TIN MÌNH ĐI!!!

Ta có: a d → = (2; −1; 4)
Xét điểm B(–3 + 2t; 1 – t; –1 + 4t) thì AB → = (1 + 2t; 3 − t; −5 + 4t)
AB ⊥ d ⇔ AB → . a d → = 0
⇔ 2(1 + 2t) − (3 − t) + 4(−5 + 4t) = 0 ⇔ t = 1
Suy ra AB → = (3; 2; −1)
Vậy phương trình của
∆
là 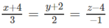
bạn trình bày vào vở như sau
chọn một đường, cho cắt với 3 đường còn lại sẽ có 3 x 4 giao điểm nhưng vì mỗi giao điểm được tính 2 lần nên số giao điểm thực tế là
3 x 4 : 2 = 6 ( giao điểm )
( tick mình nha, sau này có bài gì khó, cứ nhắn tin cho mình , nếu được mình sễ giúp. ok)
Kho..................wa.....................troi.....................thi......................lanh.................ret.......................ai........................tich..........................ung.....................ho........................minh.....................cho....................do....................lanh