Một sóng cơ lan truyền trên một sợi dây rất dài với biên độ không đổi. M, N, P là 3 điểm trên dây sao cho N là trung điểm của MP. Tại thời điểm t1 li độ dao động của M, N, P lần lượt là – 3,9 mm; 0 mm; 3,9 mm. Tại thời điểm t2 li độ của M và P đều bằng 5,2 mm; khi đó li độ của N là
A. 6,5 mm.
B. 0
C. 1,3 mm
D. 9,1 mm







Đáp án A
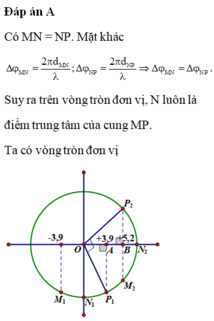
Có MN = NP. Mặt khác Δ φ M N = 2 π d M N λ ; Δ φ N P = 2 π d N P λ ⇒ Δ φ M N = Δ φ N P . Suy ra trên vòng tròn đơn vị, N luôn là điểm trung tâm của cung MP.
Ta có vòng tròn đơn vị
Từ t1 đến t2, điểm N quét 1 góc 90 độ. Vì 3 điểm M, N, P dao động cùng tần số góc, ta suy ra M và P cũng quét 1 góc 90 độ. Suy ra góc P1OP2 = 900. Dễ dàng chứng minh được tam giác P1OA bằng tam giác OP2B (cạnh huyền – góc nhọn), suy ra OA = P2B = 3,9 (cm).
Áp dụng Pytago cho tam giác P2OB, ta có: O P 2 = P 2 B 2 + O B 2 = 6 , 5 ( c m )
Suy ra biên độ dao động A = 6,5 cm. Tại t2, N nằm ở biên (điểm N2 trên hình vẽ) nên li độ của N sẽ là xN = + 6,5 (cm)