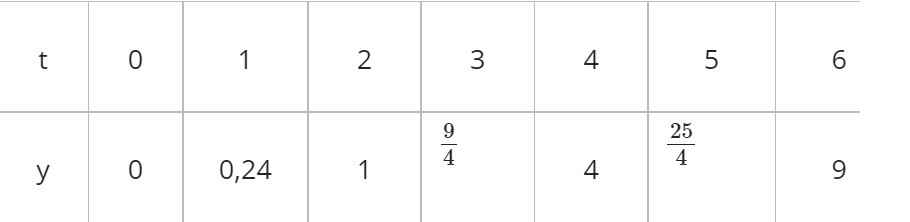
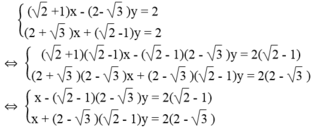Đố : Một hòn bi lăn trên một mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi công thức y = a t 2 , t tính bằng giây, y tính bằng mét. Kết quả kiểm nghiệm được cho bởi bảng sau :
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 4 |
Biết rằng chỉ có một lần đo không cẩn thận, hãy xác định hệ số a và đố em biết lần nào đo không cẩn thận ?