Cho cấp số cộng có tổng n số hạng đầu là S n = 3 n 2 + 4 n với n ∈ ℕ + . Giá trị của số hạng thứ 10 của cấp số cộng là
A. u 10 = 55.
B. u 10 = 67.
C. u 10 = 59.
D. u 10 = 61.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi số hạng đầu và công sai u 1 , d ta có S n = n 2 2 u 1 + n - 1 d = 3 n 2 + 4 n
⇒ 2 u 1 - d + n d = 8 + 6 n ⇒ 2 u 1 - d = 8 d = 6 ⇒ u 1 = 7 d = 6 ⇒ u 10 = 61 .

Chọn B
Ta có: S n = 3 n 2 + 4 n = n ( 7 + 6 n + 1 ) 2
⇒ u n = 6 n + 1 ⇒ u 10 = 61

Phương pháp:
S n = n u 1 + n ( n - 1 ) d 2
Cách giải:
Ta có:
![]()
⇒ S 20 = n u 1 + n ( n - 1 ) 2 d = - 320
Chọn C

Đáp án C
Ta có: S n = 2 u 1 + n − 1 d n 2 = d n 2 2 + u 1 − d 2 n = 5 n 2 + 3 n ⇒ d 2 = 5 u 1 − d 2 = 3 ⇔ d = 10 u 1 = 8 .

\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d=n\left(n.\dfrac{d}{2}+u_1-\dfrac{d}{2}\right)=n\left(n+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{d}{2}=1\\u_1-\dfrac{d}{2}=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=5\\d=1\end{matrix}\right.\)
\(u_n=5+1.\left(n-1\right)=n+4\)

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
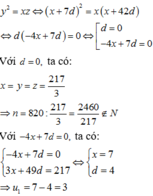
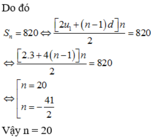
Đáp án D.