Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB=a, AC=2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC?
![]()
![]()
![]()
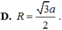
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Kẻ hinh chữ nhật A B C D như hình vẽ bên ⇒ S D ⊥ A B C D
Diện tích tam giác ABC là S A B C = 1 2 . A B . A C = a 2
Suy ra V S . A B C = 1 3 . S D . S Δ A B C = a 2 3 . S D = 2 3 a 3 ⇒ S D = 2 a .
Bán kính mặt cầu ngoại tiếp khối chóp S . A B D C là
R = R A B D C 2 + S D 2 4 = a 5 2 2 + 2 a 2 4 = 3 a 2
Vậy bán kính mặt cầu cần tính là R = 3 a 2 .

Đáp án B.
Gọi H là hình chiếu vuông góc của S trên (ABC)
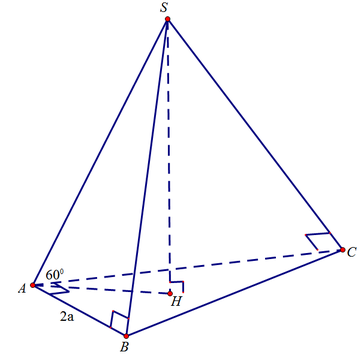
Ta có A C ⊥ S H C ⇒ A C ⊥ H C ⇒ H C / / A B .
Tương tự A B ⊥ S H B ⇒ A B ⊥ H B ⇒ H B / / A C
Vậy H là đỉnh thứ tư của hình vuông BACH như hình vẽ sau:
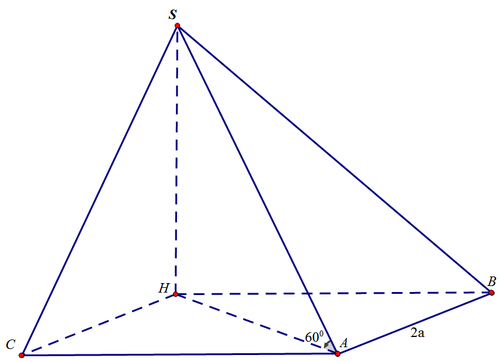
Khi ấy, ta có: A H = 2 a 2 ⇒ S H = 2 a 6
⇒ V S . A B H C = 1 3 S H . S A B H C = 1 3 2 a 6 .4 a 2 = 8 6 a 3 3
⇒ V S . A B C = 1 2 V S . A B H C = 4 6 a 3 3

Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)