Tất cả các giá trị của tham số m để hàm số y = (m-1) x 4 đạt cực đại tại x = 0 là
A. m < 1.
B. m > 1.
C. không tồn tại m.
D. m = 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Đặt y = f ( x ) = 1 3 x 3 - m x 2 + m 2 - m + 1 x + 1
![]()
f ' ' x = 2 x - 2 m
Hàm số đạt cực đại tại x = 1
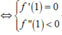
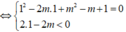

Đặt y = f ( x ) = 1 3 x 3 - m x 2 + m 2 - m + 1 x + 1
Ta có: f ' ( x ) = x 2 - 2 m x + m 2 - m ;
f ' ' ( x ) = 2 x - 2 m
Hàm số đạt cực đại tại
x=1 ⇔ f ' ( 1 ) = 0 f ' ' ( 1 ) < 0
⇔ 1 2 - 2 m . 1 + m 2 - m + 1 = 0 2 . 1 - 2 m < 0
⇔ m 2 - 3 m + 2 = 0 2 - 2 m < 0 ⇔ [ m = 1 m = 2 ⇔ m = 2 m > 1
Chọn đáp án D.

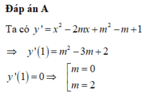
+ Với m=0 khi đó phương trình y’ = 0 sẽ có nghiệm kép nên loại.
+ Với m=2 thì khi đó phương trình y’=0 có hai nghiệm.
Chọn phương án A.

Ta có y ' = 3 x 2 - 4 x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3 . 1 2 - 4 . 1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x 3 - 2 x 2 + x + 1
Ta có y ' = 3 x 2 - 4 x + 1 , y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.
Chọn A.
Trường hợp 1: nếu m = 1 => y = 0 => hàm số không có cực trị.
Vậy m = 1 không thỏa mãn.
Trường hợp 2: nếu m ≠ 1
Ta có: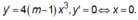
Để hàm số đạt cực đại tại x = 0 thì y’ phải đổi dấu từ (+) sang (-) qua x = 0.
Khi đó 4(m-1) < 0 ⇔ m < 1
Vậy m < 1 thỏa mãn yêu cầu bài toán.