Cho hàm số y = x 3 + bx 2 + cx + d biết đồ thị hàm số đã cho có hai điểm cực trị và đường thẳng nối hai điểm cực trị ấy đi qua điểm A(0; 1) .Hãy tìm giá trị nhỏ nhất của biểu thức T= bcd + 2bc + 3d + 20
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có y ' = 3 x 2 + 2 b x + c ⇒ y ' ' = 6 x + 2 b suy ra y ' − y ' . y ' ' 18 = 2 3 c − b 2 3 x + d − b c 9 .
Do đó, phương trình đi qua hai điểm cực trị là y = 2 3 c − b 2 3 x + d − b c 9 d .
Mà (d) đi qua gốc tọa độ O ⇒ d − b c 9 = 0 ⇔ b c = 9 d . Khi đó T = 9 d 2 + 12 d ≥ − 4.
Chú ý: Hàm số y = a x 3 + b x 2 + c x + d có phương trình đt đi qua hai điểm cực trị là f x = y − y ' . y ' ' 18 a .

Chọn đáp án D
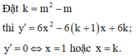
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
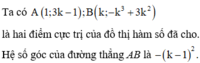
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi
