Đáp án D

Đồ thị hàm số  y = 1 2 x - 3  có hai đường tiệm cận đứng và một đường tiệm cận ngang

Đồ thị hàm số  y = x + x 2 + x + 1 x   có 1 tiệm cận đứng là x = 0 

Mặt khác  lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0  nên đồ thị hàm số có 2 tiệm cận ngang

Xét hàm số  y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2  suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng

Lời giải:

TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)

\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)

Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$

\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)

Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths

Vậy có tổng 3 TCN và TCĐ

Chọn C.

Với  đồ thị hàm số y =  a x + 1 b x - 2  nhận đường thẳng x = 2 b  làm tiệm cận đứng

Theo đề bài: x = 2 là tiệm cận đứng của đồ thị nên 

Với b ≠ 0 đồ thị hàm số y =  a x + 1 b x - 2  nhận đường thẳng y =  a b  làm tiệm cận ngang.

Theo đề bài: y = 3 là tiệm cận ngang của đò thị hàm số nên 

Vậy a + b = 4.

Chọn đáp án C

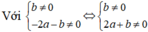
thì đồ thị hàm số y = a x + 1 b x - 2  có hai đường tiệm cận:

Đường tiệm cận đứng là x = 2 b  và đường tiệm cận ngang là  y = a b

Từ giả thiết bài toán ta có:

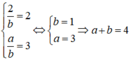
Đáp án là D.

  Đồ thị có tiệm cận đứng và tiệm cận ngang lần lượt là: x = 2 ; y = 2.

Đáp án là D

đường tiệm cận đứng và ngang.

Chọn đáp án C.