Cho hàm số y=f(x) liên tục và xác định trên ℝ có bảng biến thiên như sau:
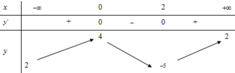
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại x=-5.
B. Hàm số có bốn điểm cực trị.
C. Hàm số đạt cực tiểu tại x=2.
D. Hàm số không có cực đại.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Xét hàm số ![]() .
.
Có ![]()
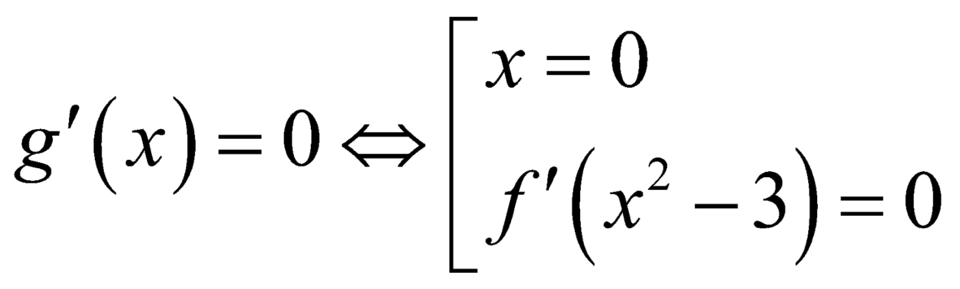
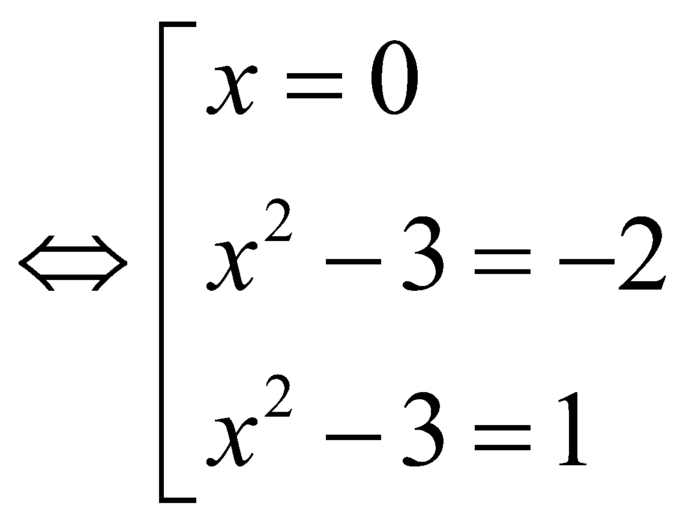
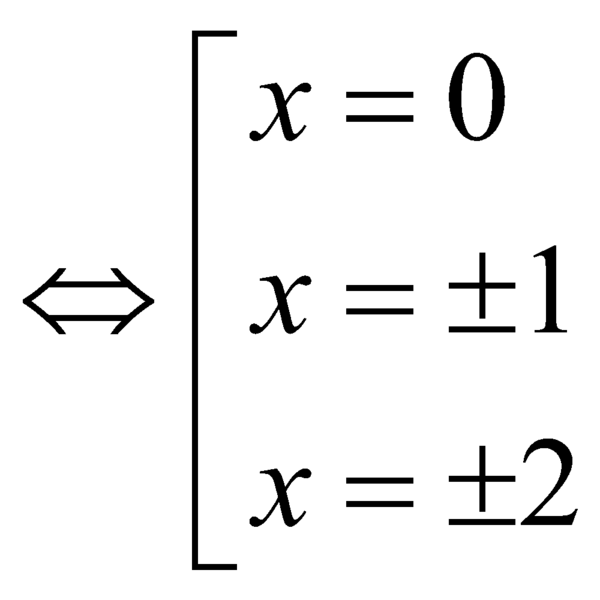 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
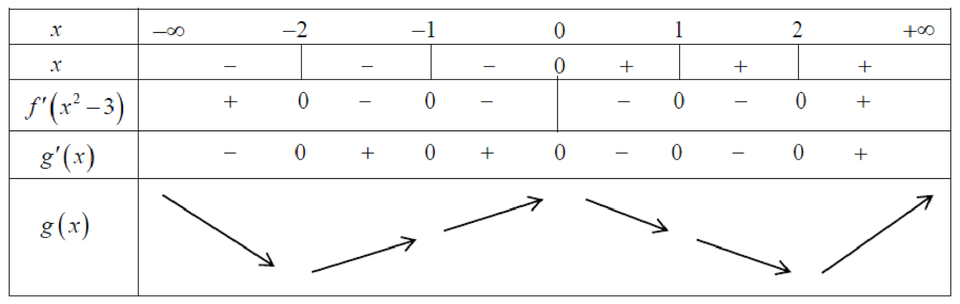
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????

Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 hàm số đạt cực tiểu tại x = 4, y C T = - 3 Do đó phương án đúng là D.


Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Dựa vào bảng biến thiên, ta thấy đạo hàm đổi dấu từ âm sang dương khi đi qua x=2 nên hàm số y=f(x) đạt cực tiểu tại điểm x=2

Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 ; hàm số đạt cực tiểu tại x = 4 , y C T = − 3. Do đó phương án đúng là D.
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhầm với giá trị cực tiểu của hàm số.
Phương án B: Sai do HS nhầm với giá trị cực đại của hàm số.
Phương án C: Sai do HS nhầm với điểm cực tiểu của hàm số.