Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
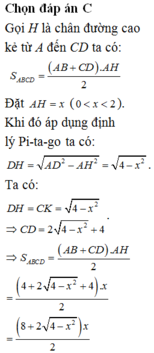
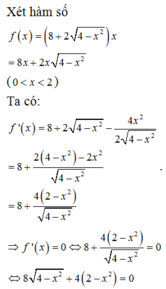
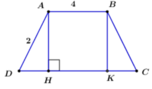
Chọn đáp án C
Phương pháp
Sử dụng công thức tính chu vi hình thang, diện tích hình thang và áp dụng định lý Pi-ta-go.
Xét hàm số, tính giá trị lớn nhất.
Cách giải
Gọi H là chân đường cao kẻ từ A đến CD ta có:
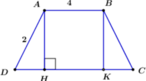
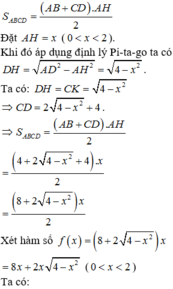
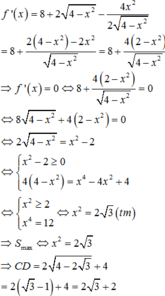
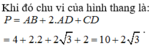
Đáp án D
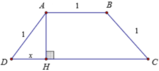
Dựng A H ⊥ C D . Đặt D H = x 0 < x < 1
Ta có: D C = 2 x + 1 ⇒ A H = 1 − x 2
S A B C D = 1 + 2 x + 1 2 1 − x 2 = 1 + x 1 − x 2 = f x ⇒ f ' x = 1 − x 2 − 1 + x x 1 − x 2 = 0 ⇔ 1 − x 2 = 1 + x x ⇔ 2 x 2 + x − 1 = 0 ⇔ x = − 1 l o a i x = 1 2 ⇒ S m a x = f 1 2 = 3 3 4 ⇔ x = 1 2
Đáp án D
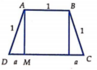
Kẻ AM vuông góc với CD tại M.
Đặt D M = a . Ta có A M = 1 − a 2 ; C D = 2 a + 1
Diện tích của hình thang là
S = 1 2 A B + C D . A M = 1 2 2 a + 2 1 − a 2 = a + 1 1 − a 2
Bài toán trở thành tìm giá trị lớn nhất của hàm số f a = a + 1 1 − a 2 trên (0;1)
Sử dụng chức năng TABLE của máy tính ta nhập
Nhìn vào bảng giá trị ta thấy giá trị lớn nhất của hàm số ≈ 1,299 . So sánh với các phương án chỉ thấy D thỏa mãn, ta chọn D.
-Gọi hình thang là ABCD, đáy nhỏ AB, đáy lớn CD, có AC⊥AD.
-Từ đỉnh A kẻ đường cao AH của hình thang. Khi đó, DH = \(\frac{50-14}{2}=18\) (cm) và CH = 50 - 18 = 32 (cm)
-Xét tam giác ACD vuông tại A, đường cao AH có:
\(AH^2=HD.HC=18.32=576\Rightarrow AH=24\)(cm)
-Xét tam giác AHD vuông tại H: \(AD=\sqrt{AH^2+DH^2}=\sqrt{24^2+18^2}=30\) (cm)
-Đã có hết các cạnh và đường cao của hình thang, áp dụng công thức tính ra chu vi và diện tích.
