Có bao nhiêu giá trị nguyên m để bất phương trình 2 2 x 2 + m x + 1 + 15 ≤ 2 − m + 8 x 2 − 3 x + 2 nghiệm đúng với ∀ x ∈ 1 ; 3 ?
A. 0
B. 1
C. 2
D. Vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(mx^2-2\left(m+2\right)x+2m-1< 0\)
\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)
\(a=m\ne0\)
\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)
\(\Delta=4m^2+8m+4-8m^2+4m\)
\(\Delta=12m-4m^2+4\)
\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)
\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)
vậy m vô số nghiệm để bpt vô nghiệm

\(\Leftrightarrow\left(x-3\right)^2+2\left(m+2\right)\left|x-3\right|+m^2+4m+3>0\)
Đặt \(\left|x-3\right|=t\Rightarrow0\le t< 5\)
\(\Rightarrow t^2+2\left(m+2\right)t+m^2+4m+3>0\) ;\(\forall t\in[0;5)\)
\(\Leftrightarrow\left(t+m+1\right)\left(t+m+3\right)>0\)
\(\Rightarrow-m-3< t< -m-1\)
Pt nghiệm đúng với mọi \(t\in[0;5)\) khi và chỉ khi
\(\left\{{}\begin{matrix}0>-m-3\\5\le-m-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m\le-5\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn

ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m

Đáp án là B
Phương trình tương đương với
![]()
![]()
![]()
Xét hàm ![]() Ta có
Ta có ![]() đồng biến
đồng biến
Mà ![]() suy ra
suy ra
![]()
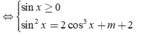
![]()
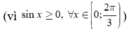
![]()
![]()
Đặt u = cosx, 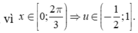
Khi đó phương trình trở thành ![]()
Xét ![]()
![]()
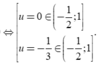
Bảng biến thiên
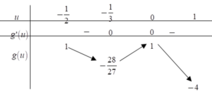
Dựa vào bảng biến thiên suy ra phương trình có nghiệm khi
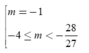
![]()
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?

Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
Đáp án B.