Với điều kiện nào của tham số m cho dưới đây, đường thẳng d:y=-3x+m cắt đồ thị (C) của hàm số y = 2 x + 1 x - 1 tại hai điểm phân biệt A và B sao cho trọng tâm tam giác OAB thuộc đồ thị (C) với O(0;0) là gốc tọa độ?
A.![]()
B. ![]()
C. ![]()
D. Với mọi m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình hoành độ giao điểm của (C) và d là:
![]() (*)
(*)
![]()
(C) cắt d tại hai điểm phân biệt ![]() có hai nghiệm phân biệt x1, x2
có hai nghiệm phân biệt x1, x2
![]()
![]()
Gọi ![]() và
và ![]() là các giao điểm của (C) và d với
là các giao điểm của (C) và d với 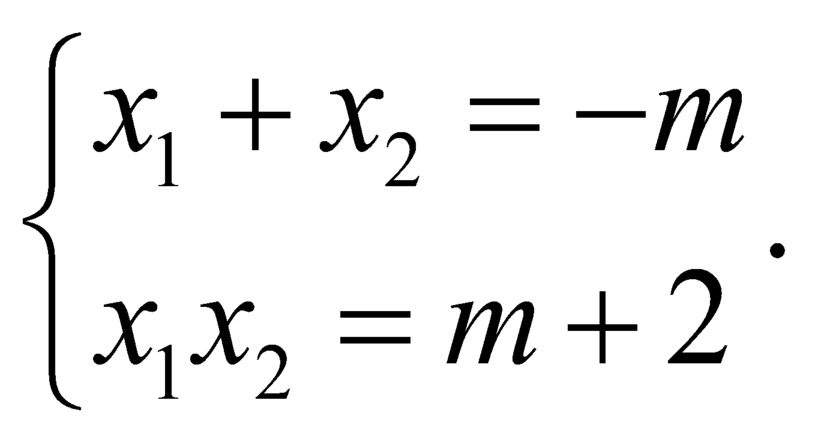
Khi đó
![]()
![]()
![]()
![]()
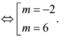
Ngoài ra, ta có thể kiểm tra sau khi có ![]() Khi đó, ta loại các phương án m = 1; m = 5
Khi đó, ta loại các phương án m = 1; m = 5
Thử một phương án m = -2, ta được phương trình:
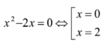
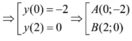
![]()

Đáp án là B.
Phương trình hoàng độ giao điểm của
C & d : x + m 2 x − 1 = − x + 1 ; x ≠ 1 2
⇔ 2 x 2 + 2 m x − m − 1 = 0 (1)
C & d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .
Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0 ⇔ m ∈ ℝ .

Đáp án B
Phương pháp: Xét phương trình hoành độ giao điểm, đưa phương trình về phương trình bậc hai và sử dụng công thức tính khoảng cách, định lý Vi-et cho phương trình bậc hai để tìm m
Cách giải:
Xét phương trình hoành độ
giao điểm:

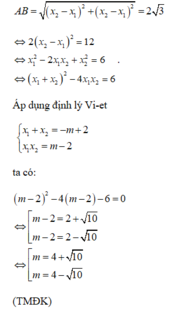
Vậy m = 4 ± 10

Lời giải:
PT hoành độ giao điểm:
$\frac{-4x+12}{x+1}=2x+m$
$\Rightarrow -4x+12=(2x+m)(x+1)$
$\Leftrightarrow 2x^2+x(m+6)+m-12=0(*)$
Ta thấy:
\(2(-1)^2+(-1)(m+6)+m-12=-16\neq 0\)
$\Delta (*)=(m+6)^2-8(m-12)=m^2+4m+132=(m+2)^2+128>0$ với mọi $m$
$\Rightarrow (*)$ luôn có 2 nghiệm pb khác -1 với mọi $m$
Tức là $(d)$ cắt $(C)$ tại 2 điểm phân biệt với mọi $m$ (đpcm)
Đáp án B
Phương trình hoành độ giao điểm của (C) và d:
Khi đó d cắt (C) tại hai điểm phân biệt A và B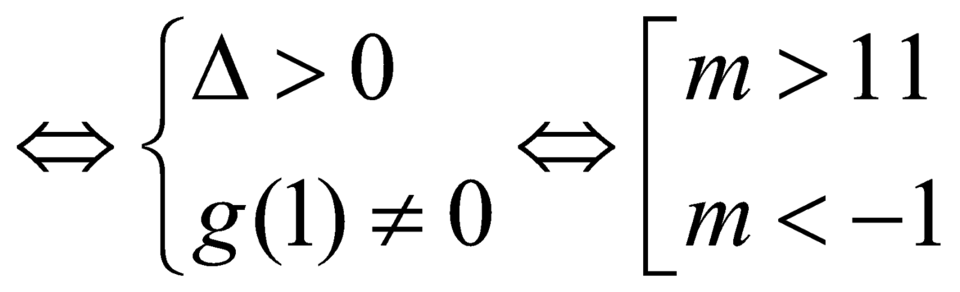 (*)
(*)
Gọi G là trọng tâm của tam giác OAB ta có O G → = 2 3 O I ⇀ với I là trung điểm của AB.
Tìm được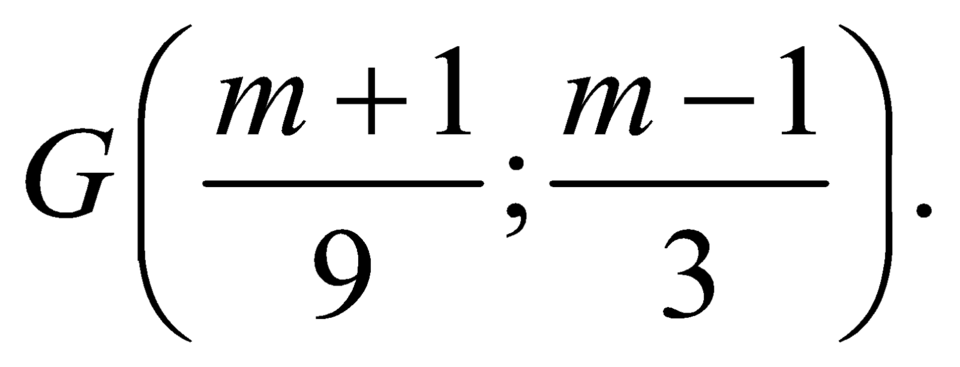 Do đó,
Do đó, 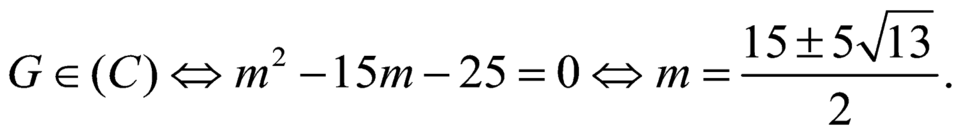
Chú ý: Để làm bài này khi thực hiện trắc nghiệm, ta nên tìm đến điều kiện (*), sau đó loại các kết quả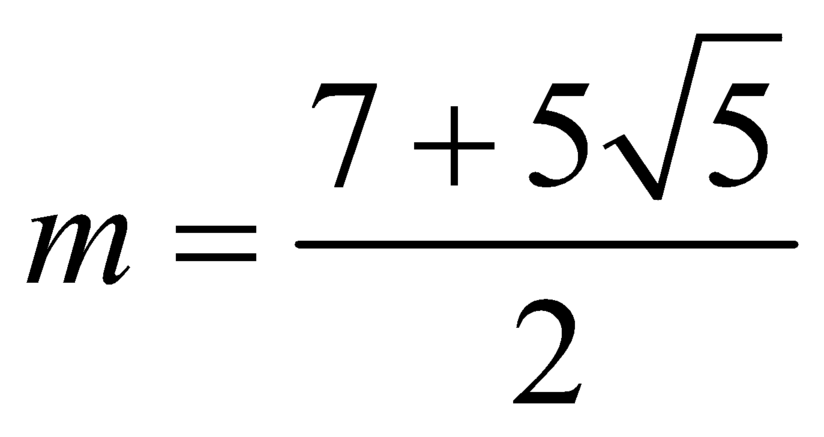 và
và 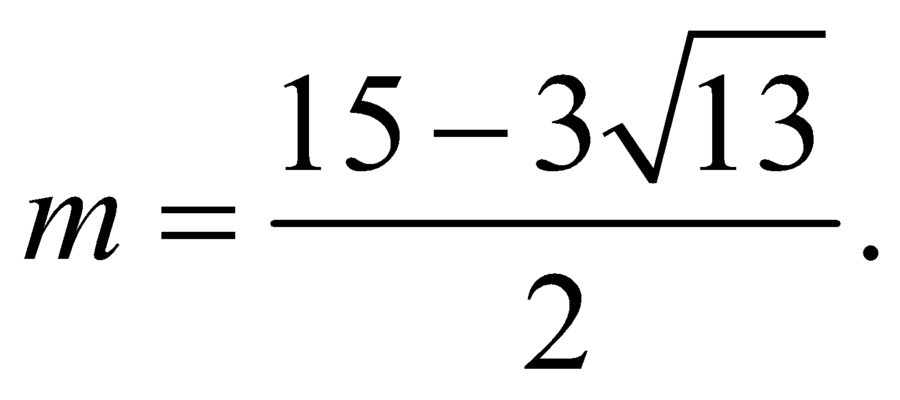 Sau đó, lấy một giá trị nguyên của m để kiểm tra giả thiết bài cho, giả sử với m = -2.
Sau đó, lấy một giá trị nguyên của m để kiểm tra giả thiết bài cho, giả sử với m = -2.
Ta còn lại đáp số của bài toán.