Cho hàm số f x = x + 2 x 2 - 9 có đồ thị như trên hình 53.
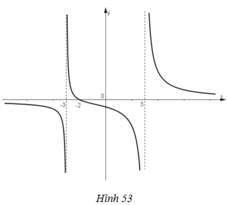
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x → - ∞ , x → 3 - , x → - 3 +
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: f(x0)=x0+1
\(\lim\limits_{x\rightarrow x0}f\left(x\right)=x_0+1\)=f(x0)
=>HS f(x) liên tục tại điểm x0
b: Đồ thị hàm số là một đường thẳng liền mạch với mọi x thực

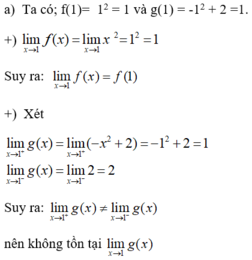
b)
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.

Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.
Hình 14b đồ thị bị chia làm hai nhánh:
- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.
- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.
Vậy hàm số liên tục trên từng khoảng xác định.
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

a)

Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)
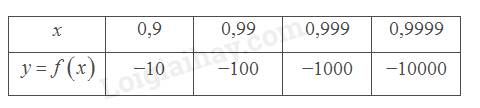
Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.

- Khi x → (-3)+, đồ thị hàm số là một đường cong đi lên từ phải qua trái.
- Do đó: 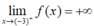
- Tương tự như vậy ta có:
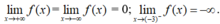
Do đó chọn đáp án C.

Chọn C.
Khi x → -3+, đồ thị hàm số là một đường cong đi lên từ phải qua trái. Do đó ![]() .
.
Tương tự như vậy ta có ![]()
a) Quan sát đồ thị nhận thấy:
f(x) → 0 khi x → -∞
f(x) → -∞ khi x → 3-
f(x) → +∞ khi x → (-3)+.