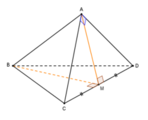
Cho tứ diện ABCD có AB = 2a, tam giác BCD vuông tại C, BD = 2a, BC = a và 2 A C 2 - A D 2 = 6 a 2 Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng
A. 30 °
B. 90 °
C. 45 °
D. 60 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Loại phương án A và B vì BC và CD không phải là hình chiếu của CM trên (BCD)
Phương án C đúng vì :

Đáp án C

Đáp án D
![]()
nên ∆ BCDlà tam giác đều.
![]()
nên theo định lý Py-ta-go đảo, ta có ∆ ACD vuông cân tại A .
Khi đó, gọi M là trung điểm CD thì: AM ⊥ CD và BM ⊥ CD Ta có:
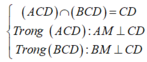
![]()
∆
BCD đều có đường cao
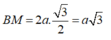
∆
ACD vuông cân tại A nên trung tuyến
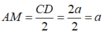
Áp dụng định lý hàm cos trong
∆
AMB, ta có:
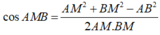
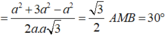
![]()
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) có số đo bằng 30 o

Đáp án B
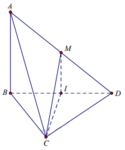
Gọi I là trung điểm BD. Khi đó I C M ^ = φ
Ta có: tan φ = I M C I = a a 3 2 = 2 3 3

AB vuông góc BC
AB vuông góc BD
=>AB vuông góc (BCD)
=>AB vuông góc CD
BC vuông góc CD
AB vuông góc CD
=>CD vuông góc (BCA)
=>CD vuông góc BH
=>(BH;CD)=90 độ
Gọi F là trung điểm cạnh AD có
A B / / E F ⇒ A B , E C = E F , E C
Tam giác ∆ E F C có
c o s ∠ F E C = E F 2 + E C 2 - F C 2 2 . E F . E C
Vậy góc giữa hai đường thẳng AB và EC bằng 60 °
Chọn đáp án D.