Trong không gian Oxyz cho bốn điểm A(3;0;0),B(0;2;0),C(0;0;6) và D(1;1;1) Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất, hỏi ∆ đi qua điểm nào trong các điểm dưới đây? A. M(5;7;3) B. M(3;4;3) C. M(7;13;5) D. ...
Đọc tiếp
Trong không gian Oxyz cho bốn điểm A(3;0;0),B(0;2;0),C(0;0;6) và D(1;1;1) Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất, hỏi ∆ đi qua điểm nào trong các điểm dưới đây?
A. M(5;7;3)
B. M(3;4;3)
C. M(7;13;5)
D. M(-1;-2;1)
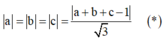
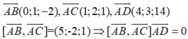
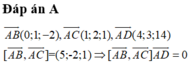
Phương trình mặt phẳng (ABC) là x 3 + y 2 + z 6 = 1 →2x+3y+z-6=0
Dễ thấy D ϵ (ABC). Gọi H,K,I lần lượt là hình chiếu của A,B,C trên ∆.
Do ∆ là đường thẳng đi qua D nên AH≤ AD,BK≤ BD,CI≤ CD.
Vậy để khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất thì ∆ là đường thẳng đi qua D và vuông góc với (ABC). Vậy phương trình đường thẳng ∆ là x = 1 + 2 t y = 1 + 3 t ( t ∈ ℝ ) z = 1 + t . Kiểm tra ta thấy điểm M(5;7;3) ϵ ∆
Đáp án A