Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. - ∞ ; 3
B. - ∞ ; 3
C. ( 3 2 ; + ∞ )
D. ( - ∞ ; 3 2 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

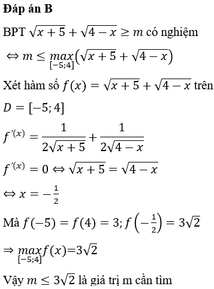

Đáp án B
Điều kiện x + 5 ≥ 0 4 − x ≥ 0 ⇔ − 5 ≤ x ≤ 4
Xét hàm số f x = x + 5 + 4 − x ; x ∈ − 5 ; 4
Ta có:
f ' x = 1 2 x + 5 − 1 2 4 − x ; f ' x = 0 ⇔ 4 − x = x + 5 ⇔ x = − 1 2
Tính các giá trị f − 5 = 3 ; f 4 = 3 ; f − 1 2 = 3 2
⇒ max − 5 ; 4 f x = f − 1 2 = 3 2
Vậy để phương trình m ≤ f x có nghiệm m ≤ max − 5 ; 4 f x ⇔ m ≤ 3 2

Chọn đáp án D
Số nghiệm của phương trình f ( x ) = m bằng
số giao điểm của đồ thị hàm số y = f ( x ) với
đường thẳng y = m
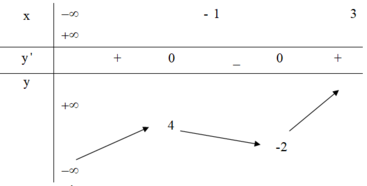
Từ bảng biến thiên suy ra phương trình có 3 nghiệm phân biệt khi − 2 < m < 4.

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-4t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt dương:
\(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4-m>0\\4>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 4\)