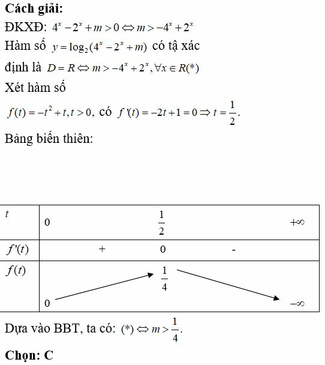
Hàm số y = log 2 ( 4 x - 2 x + m ) có tập xác định là D = R khi
A. m ≤ 1 4
B. m < 1 4
C. m > 1 4
D. m ≥ 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm có TXĐ là R khi và chỉ khi: \(\left(m-2\right)x^2+\left(m-2\right)x+4\ge0;\forall x\)
- Với \(m=2\) thỏa mãn
- Với \(m\ne2\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\Delta=\left(m-2\right)^2-16\left(m-2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\\left(m-2\right)\left(m-18\right)\le0\end{matrix}\right.\) \(\Rightarrow2< m\le18\)
Kết hợp lại ta được: \(2\le m\le18\)

Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
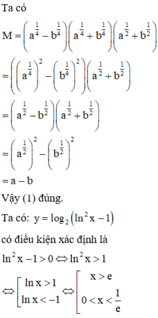
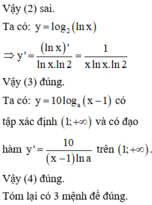

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

\(a,D=R\\ b,2x-3>0\\ \Rightarrow x>\dfrac{3}{2}\\ \Rightarrow D=(\dfrac{3}{2};+\infty)\\ c,-x^2+4>0\\ \Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\\ \Rightarrow D=\left(-2;2\right)\)