Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 − 1 2 m 2 + 1 x 2 + 3 m − 2 x + m đạt cực đại tại điểm x=1
A. m=-1
B. m=2
C. m=1
D. m=-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
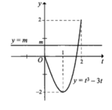
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()

Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)
Đáp án B
Ta có y ' = x 2 − m 2 + 1 x + 3 m − 2 , y ' ' = 2 x − m 2 − 1
Hàm số đạt cực đại tại x = 1 ⇒ y ' 1 = 0 ⇔ 1 − m 2 + 1 + 3 m − 2 = 0 ⇔ m = 1 m = 2
Với m = 1 ⇒ y ' ' = 2 x − 2 ⇒ y ' ' 1 = 0
Với m = 2 ⇒ y ' ' = 2 x − 5 ⇒ y ' ' 1 = − 3
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 2