Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn − 1 ; 2 . Tìm tổng bình phương của M và m
A. 250.
B. 100.
C. 509.
D. 289.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f ( x ) = 2 x 3 + 3 x 2 - 1 ⇒ f ' ( x ) = 6 x 2 + 6 x ; f ' ( x ) = 0 ⇔ [ x = 0 ( k t m ) x = - 1 ( t m )
Hàm số f(x) liên tục trên - 2 ; - 1 2 ,
có f ( - 0 ) = - 5 ; f ( - 1 ) = 0 ; f - 1 2 = - 1 2
⇒ m = m i n - 2 ; - 1 2 f ( x ) = - 5 ; M = m a x - 2 ; - 1 2 f ( x ) = 0 ⇒ P = M - m = 5
Chọn đáp án C.

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 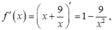
![]()
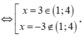
Có ![]()
![]()
Vậy m + M = 16.
Đáp án A
Ta có: y ' = 6 x 2 + 6 x − 12 ⇒ y ' = 0 ⇔ x = 1 x = − 2
Suy ra: y − 1 = 15 , y 1 = − 5 , y 2 = 6 ⇒ M = 15 m = − 5 ⇒ M 2 + m 2 = 250.