Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
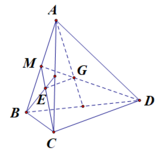
Gọi M là trung điểm của AB .
Có G là trọng tâm tam giác ABC nên G M D M = 1 3
Và E là trọng tâm tam giác ABC nên E M C M = 1 3
Áp dụng định lý Ta – lét có : G E // D C .
a: Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABD có
AO,DM là các đường trung tuyến
AO cắt DM tại G
Do đó: G là trọng tâm của ΔABD
b: Xét ΔABD có
AO là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}\cdot AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}AC\)
Ta có: CG+GA=CA
=>\(GA+\dfrac{1}{3}AC=AC\)
=>\(GA=\dfrac{2}{3}AC\)
\(\dfrac{AG}{GA}=\dfrac{\dfrac{1}{3}AC}{\dfrac{2}{3}AC}=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\)
=>GA=2AG
Đáp án B
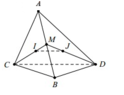
Gọi M là trung điểm của AB
Tam giác ABC có trọng tâm I suy ra M I M C = 1 3
Tam giác ABC có trọng tâm J suy ra M J M D = 1 3
Khi đó M I M C = M J M D ⇒ I J / / C D (định lí Talet)
Đáp án là D