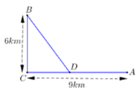
Một công ty muốn làm một đường ống dẫn dầu từ một kho A ở trên bờ đến một vị trí B trên một hòn đảo. Hòn đảo cách bờ biển 6 km. Gọi C là điểm trên bờ sao cho BC vuông góc với bờ biển. Khoảng cách từ A đến C là 9 km. Người ta cần xác định một vị trí D trên AC để lắp ống dẫn theo đường gấp khúc ADB. Để số tiền chi phí thấp nhất mà công ty phải thì khoảng cách từ A đến D là bao nhiêu km, biết rằng chi phí để hoàn thành mỗi km đường ống trên bờ là 100 triệu đồng và dưới nước là 260 triệu đồng.
A. 8 km
B. 5 km
C. 7,5 km
D. 6,5 km





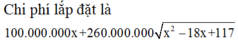
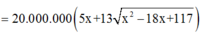

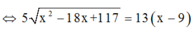
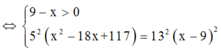


Đáp án là D.
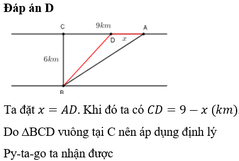
Đặt C D = x , x ∈ 0 ; 9 . Ta có B D = x 2 + 36
Chi phí xây dựng đường ống f x = 100 9 − x + 260 x 2 + 36
Ta có:
f ' x = − 100 + 260 x x 2 + 36 , c h o f ' x = 0 ⇔ 5 x 2 + 36 = 13 x ⇔ x = 5 2
f 0 = 2460 ; f 5 2 = 2340 ; f 9 ≈ 2812 , 33
Chi phí thấp nhất x = 5 2 . Khoảng cách từ A đến D là: 6,5km