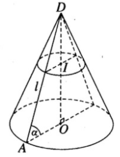
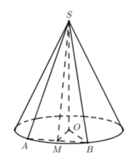
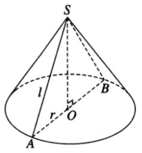
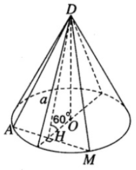
Cho hình nón tròn xoay có thiết diện qua đỉnh là một tam giác vuông cân. Hãy chọn câu sai trong các câu sau:
A. Hai đường sinh tùy ý thì vuông góc với nhau
B. Đường cao bằng tích bán kính đáy và tan 45 °
C. Đường sinh hợp với trục góc 45 °
D. Đường sinh hợp với đáy góc 60 °





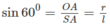
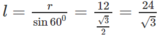
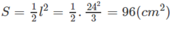


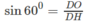
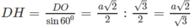
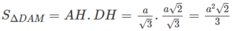
Phương pháp:
Sử dụng mối quan hệ góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng.
Sử dụng tính chất hình nón, tính chất tam giác vuông cân.
Cách giải:
Hình nón đỉnh S có thiết diện đi qua đỉnh là tam giác vuông cân SAB khi đó xét tam giác vuông SHB có đường cao