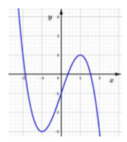
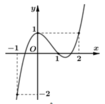
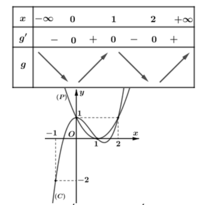
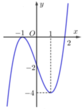
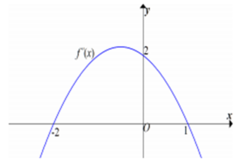
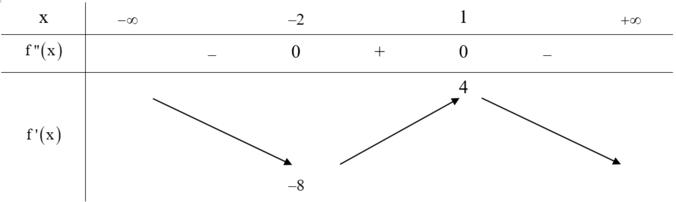
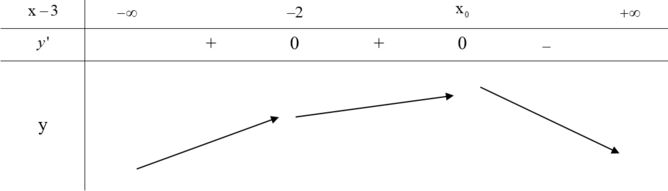
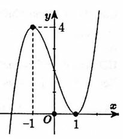
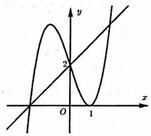
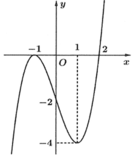
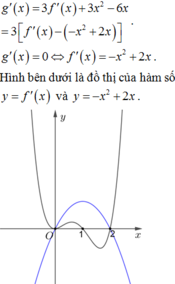
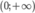Cho hàm số y=f( x ) có đạo hàm liên tục trên ℝ và có đồ thị của hàm y= f ' ( x ) như hình vẽ
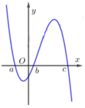
Xét hàm số ![]() Mệnh đề nào dưới đây sai?
Mệnh đề nào dưới đây sai?
A. Hàm số f (x) đạt cực đại tại x=2
B. Hàm số f (x) nghịch biến trên - ∞ ; 2
C. Hàm số f(x) đồng biến trên ( 2; + ∞ )
D. Hàm số f(x) đồng biến trên ( -1; 0)

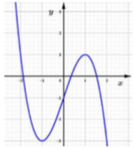
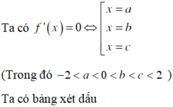


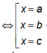
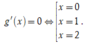


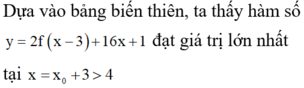


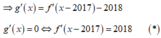

Đáp án D
Dễ thấy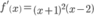
Do f (x) đổi dấu từ âm sang dương khi qua điểm x = 2 nên f (x) đạt cực trị tại x =2
Hàm số f (x) nghịch biến trên do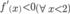
Đặt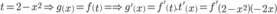
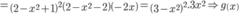
đồng biến trên