Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi G 1 , G 2 , G 3 , G 4 là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện G 1 G 2 G 3 G 4 .
A. V = 2 4
B. 2 18
C. V = 2 32
D. V = 2 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
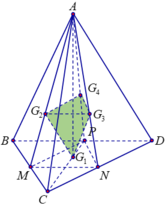
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay 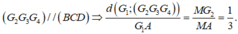
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
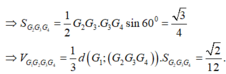

Đáp án D
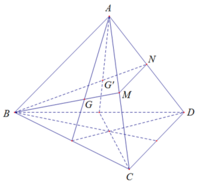
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

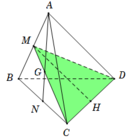
Gọi M; N lần lượt là trung điểm của AB và B C suy ra AN và MC cắt nhau tại G
Dễ thấy mặt phẳng (GCD) cắt đường thắng AB tại điểm M.
Suy ra tam giác MCD là thiết diện của mặt phẳng (GCD) và tứ diện.
Tam giác ABD đều, có M là trung điểm AB suy ra
Tam giác A BC đều, có

Chọn B.

Đáp án D
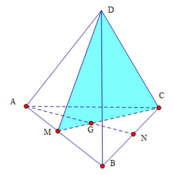
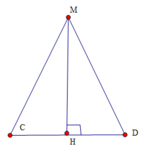
Thiết diện là tam giác cân MCD trong đó M là trung điểm AB n
Ta có D M = C M = a 3 2 ; C D = a
Gọi H là trung điểm
C D ⇒ M H = M C 2 − C H 2 = 3 a 2 4 − a 2 4 = a 2 2
S M C D = 1 2 M H . C D = 1 2 a 2 2 . a = a 2 2 4
Đáp án D