Đáp án B

Ta có 

S = 1 .2 + 2 . 3+ ...+39.40

=> 3S = 1 . 2 . ( 3 - 0 ) + 2 .3 ( 4-1)+...39 . 40 (41 - 38 )

=> 3S = 1 . 2 .3 - 0.1.2+ 2 . 3 . 4- 1.2.3+....+39.40.41-38.39.40

=> S = \(\frac{38.39.40}{3}\)

=> S = 21320

S = 1x2 + 2x3 + ... + 38x39 + 39x40

3S = 1x2x3 + 2x3x3 + ... + 38x39x3 + 39x40x3

3S = 1x2x3 + 2x3x(4-1 ) + ... + 38x39x(40-37) + 39x40x(41-38)

3S = 1x2x3 + 2x3x4 - 1x2x3 + ... + 38x39x40 - 37x38x39 + 39x40x41 - 38x39x40

3S = 39x40x41

S = 39x40x41 : 3

S = 21320

mk chỉ biết câu a  bài 2 thôi thông cảm

Bài 2:

a)x=2

a) \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{2006.2007}\)

\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2006}-\frac{1}{2007}\)

\(=1-\frac{1}{2007}\)

\(=\frac{2006}{2007}\)

CẦN GẤP NHÉ MỌI NGƯỜI

\(\Leftrightarrow3x-\left(\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{99.100}\right)=\left(\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{18.19.20}\right)\)

\(\Leftrightarrow3x-\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{99}-\frac{1}{100}\right)=\frac{1}{2}\cdot\left(\frac{1}{1.2}-\frac{1}{2.3}+....+\frac{1}{18.19}-\frac{1}{19.20}\right)\)

\(\Leftrightarrow3x-\left(1-\frac{1}{100}\right)=\frac{1}{2}\cdot\left(\frac{1}{1.2}-\frac{1}{19.20}\right)\)

\(\Leftrightarrow3x-\frac{99}{100}=\frac{1}{2}\cdot\frac{189}{380}\)

\(\Leftrightarrow3x-\frac{99}{100}=\frac{189}{760}\)

\(\Leftrightarrow3x=\frac{189}{760}+\frac{99}{100}=\frac{4707}{3800}\)

\(\Leftrightarrow x=\frac{1569}{3800}\)

\(\text{Vậy }x=\frac{1569}{3800}\)

Học sinh gương mẫu của lớp thầy Phú là đây

Đặt  t = x 2 t ≥ 0

Phương trình (1) thành  − t 2 − 2 ( 2 − 1 ) t + ( 3 − 2 2 )   = 0   ( 2 )

Phương trình (2) có  a . c = ( − 1 )   ( 3 − 2 2 ) < 0

Suy ra phương trình (2) có 2 nghiệm trái dấu

Suy ra phương trình ban đầu có 2 nghiệm phân biệt.

Đáp án cần chọn là: A

Ta có:

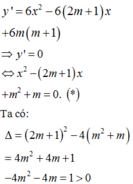
⇒ *  luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2  với mọi m.

Áp dụng hệ thức Vi-ét ta có:

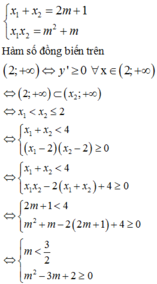
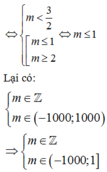
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.

Chọn B.

Số cuối là ?

Số cuối là dấu hỏi chấm.