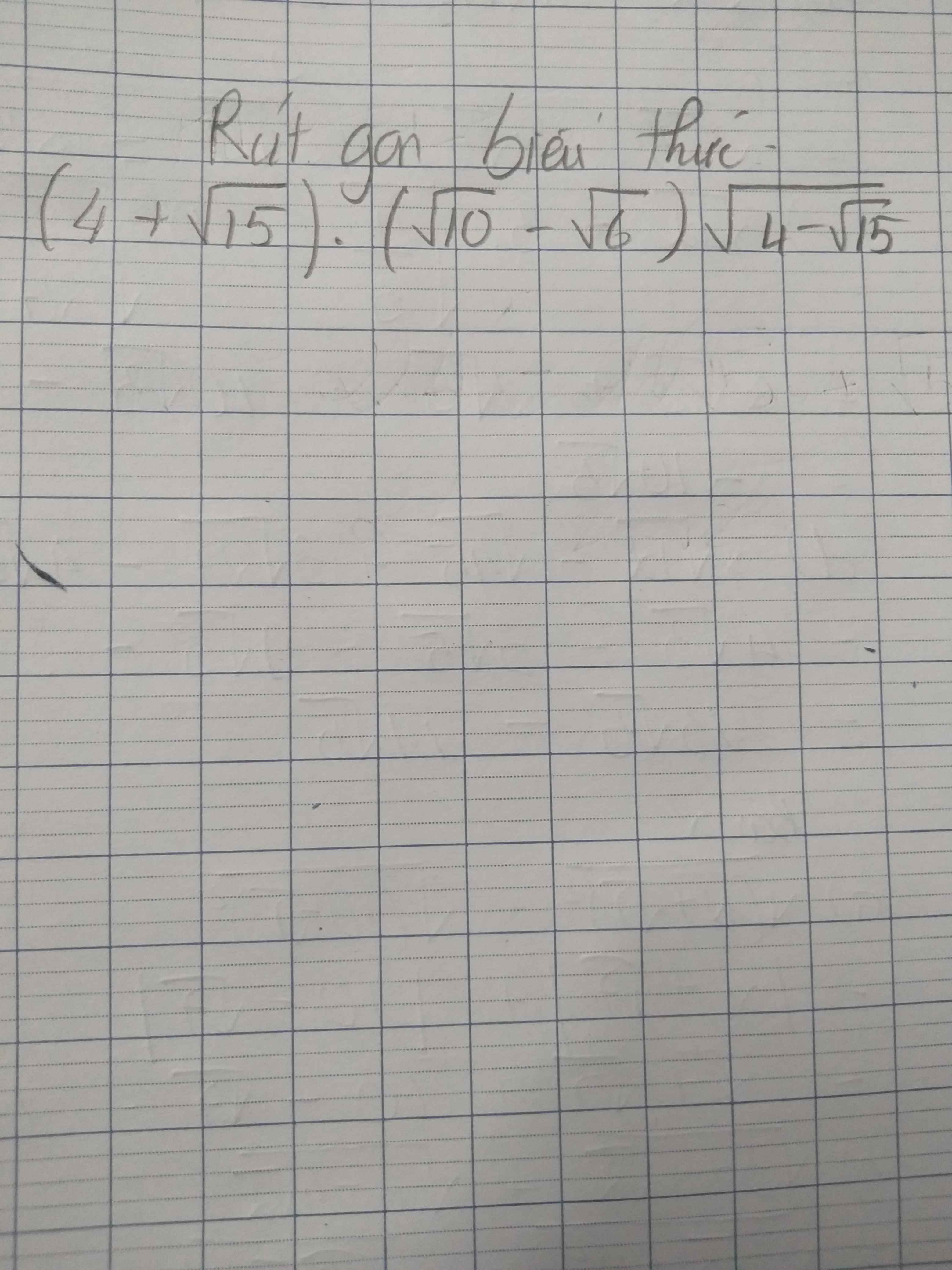Lời giải:

$\widehat{M_1}-\widehat{M_2}=\widehat{N_1}-\widehat{N_2}(1)$

$\widehat{M_1}+\widehat{M_2}=\widehat{N_1}+\widehat{N_2}(2)$ (cùng bằng $180^0$)

Lấy $(1)+(2)$ và thu gọn thì $\widehat{M_1}=\widehat{N_1}$
Mà 2 góc này ở vị trí so le trong nên $m\parallel n$

O1=O2( vì 2 góc đối đỉnh)

O3 và O4 thì làm theo cách hai góc kề bù

Vd :O1+O3=180 độ (2 góc kề bù)

Suy ra :120 độ +O3=180 độ

Vậy từ đó tính ra đc O3 ,tương tự O4 cũng vậy

À quên ,sau khi tìm đc O3 thì suy ra O4 lun vì 2 góc đó đối đỉnh nên = nhau 

Câu 1.

a) Vì hai điện tích cùng dấu nên lực tương tác của chúng là đẩy nhau.

b) Lực tương tác:

   \(F=k\cdot\dfrac{\left|q_1\cdot q_2\right|}{r^2}=9\cdot10^9\cdot\dfrac{6\cdot10^{-4}\cdot4\cdot10^{-5}}{0,06^2}=60000N\)

Câu 2.

a)Lực tương tác:

   \(F=k\cdot\dfrac{\left|q_1\cdot q_2\right|}{r^2}=9\cdot10^9\cdot\dfrac{q^2}{0,03^2}=4\cdot10^{-2}\)

   \(\Rightarrow q_1=q_2=q=6,32\cdot10^{-8}C\)

b)Để lực tương tác là \(8\cdot10^{-2}N\) cần đặt hai điện tích:

  \(F'=k\cdot\dfrac{\left|q_1q_2\right|}{r'^2}=9\cdot10^9\cdot\dfrac{4\cdot10^{-15}}{r'^2}=8\cdot10^{-2}\)

   \(\Rightarrow r'\approx0,02m=2cm\)

Câu 1:

a)Lực đẩy vì điện tích giữa chúng là cùng dấu

b)\(F=\dfrac{k\left|q_1q_2\right|}{r^2}=\dfrac{9.10^9\left|6.10^{-4}.4.10^{-5}\right|}{0,06^2}=3600\left(N\right)\)

\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{2}\sqrt{4-\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)

Mình cảm ơn bạn nhìu nha.

Bạn chụp rõ hơn được không, mờ quá

Ta có \(\widehat{ABC}=\widehat{CAH}\) ( cùng phụ vs \(\widehat{HAB}\) )

Vì tam giác HAC vuông tại H có đường trung tuyến HF

=> HF = 1/2 AC

=> HF = AF

=> tam giác AHF cân tại F

=> góc CAH = góc FHA

Mà góc CAH = góc ABC (cmt)

=> góc ABC = góc FHA

Có OH = OB

=> tam giác OHB cân tại O

=> góc OHB = góc ABC

=> góc FHA = góc OHB

Lại có: góc OHB + góc OHA = 90o

=> góc FHA + góc OHA = 90o

=> góc OHF = 90o

=> OH vuông góc FH

Mà H thuộc (O)

=> FH là tiếp tuyến của (O)