Giúp mình nha mọi người mai mình nộp rồi
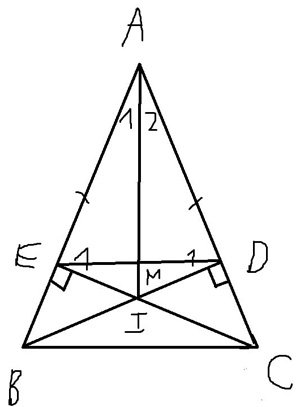
cho tam giác ABC cân tại A kẻ BD vuông góc AC tại D, CE vuông góc AB tại E, BD giao CE tại O
a) cm tam giác EAC=tam giác DAB
b) Định dạng tam giác ADE
c) OE=OD
d) Cm AO là trung trực BC, DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2016
a) Xét tam giác ABD và tam giác ACE có
góc ADB = góc AEC = 90 độ
AB=AC
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác OEB và tam giác ODC có
góc OEB = góc ODC = 90 độ
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC
=> AO la tia phân giác góc BAC
Bài mk lm như dzị ak
A
15 tháng 2 2018
a, tg ADB và tg AEC có^E1 = ^D1 = 90 độ
AB = AC
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
AB = AC
=> tg ABI = tg ACI
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD
17 tháng 2 2022
a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔBEK vuông tại E và ΔCDK vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔBEK=ΔCDK
c: Xét ΔBAK và ΔCAK có
BA=CA
AK chung
BK=CK
Do đó: ΔBAK=ΔCAK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
27 tháng 1 2022
a) Xét tam giác BCE vuông tại E và tam giác CBD vuông tại D:
BC chung.
Góc B = Góc C (Tam giác ABC cân tại A).
=> Tam giác BCE = Tam giác CBD (cạnh huyền - góc nhọn).
b) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E:
Góc A chung.
AB = AC (Tam giác ABC cân tại A).
=> Tam giác ABD = Tam giác ACE (cạnh huyền - góc nhọn).
=> Góc ABD = Góc ACE (2 góc tương ứng).
Xét tam giác BEK và tam giác CDK:
Góc EBK = Góc DCK (Góc ABD = Góc ACE).
BE = CD (Tam giác BCE = Tam giác CBD).
Góc BEK = Góc CDK (= 90o).
=> Tam giác BEK = Tam giác CDK (g - c - g).
c) Xét tam giác ABC:
BD là đường cao (BD vuông góc với AC).
CE là đường cao (CE vuông góc với AB).
BD cắt CE tại K (gt).
=> K là trực tâm.
=> AK là đường cao.
Xét tam giác ABC cân tại A: AK là đường cao (cmt).
=> AK là đường phân giác góc BAC (Tính chất các đường trong tam giác cân).
N
18 tháng 1 2021
Sửa lại đề : A < 90*
a, Chứng minh
\(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\RightarrowĐPCM\)
b, CM được :
\(\widehat{ADE}\)\(=\)\(\widehat{ACB}\)\(=\)\(\frac{180'-\widehat{BAC}}{2}\)
\(\Rightarrow DE//BC\)
c, CM được : \(\widehat{IBC}=\widehat{ICB}\)
\(\RightarrowĐPCM\)
d, Gọi M là giao điểm của AI và BC ,
CM được AI là tia phân giác của góc \(\widehat{BAC}\), từ đó \(\widehat{AMB}\)\(=90'\)
\(\RightarrowĐPCM\)
18 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
KV
15 tháng 2 2020
a, Xét 2 tam giác vuông ΔABD và ΔACE có:
AB = AC (gt);
góc A chung
⇒ ΔABD = ΔACE (cạnh huyền - góc nhọn) (đpcm)
b, ΔABD = ΔACE ⇒ AD = AE
⇒ AC - AD = AB - AE ⇒ BE = CD
Xét 2 tam giác vuông ΔBIE và ΔCID có:
BE = CD
\(\widehat{BEI}=\widehat{CDI}\) ( đối đỉnh )
⇒ ΔBEI = ΔCDI (cạnh góc vuông - góc nhọn)
28 tháng 4 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
=>ΔADB=ΔAEC
=>góc ABD=góc ACE
b: góc HBC+góc ABD=góc ABC
góc HCB+góc ACE=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc HBC=góc HCB
=>ΔBHC cân tại H
=>HB=HC>HD