Giải câu h giúp em với mọi người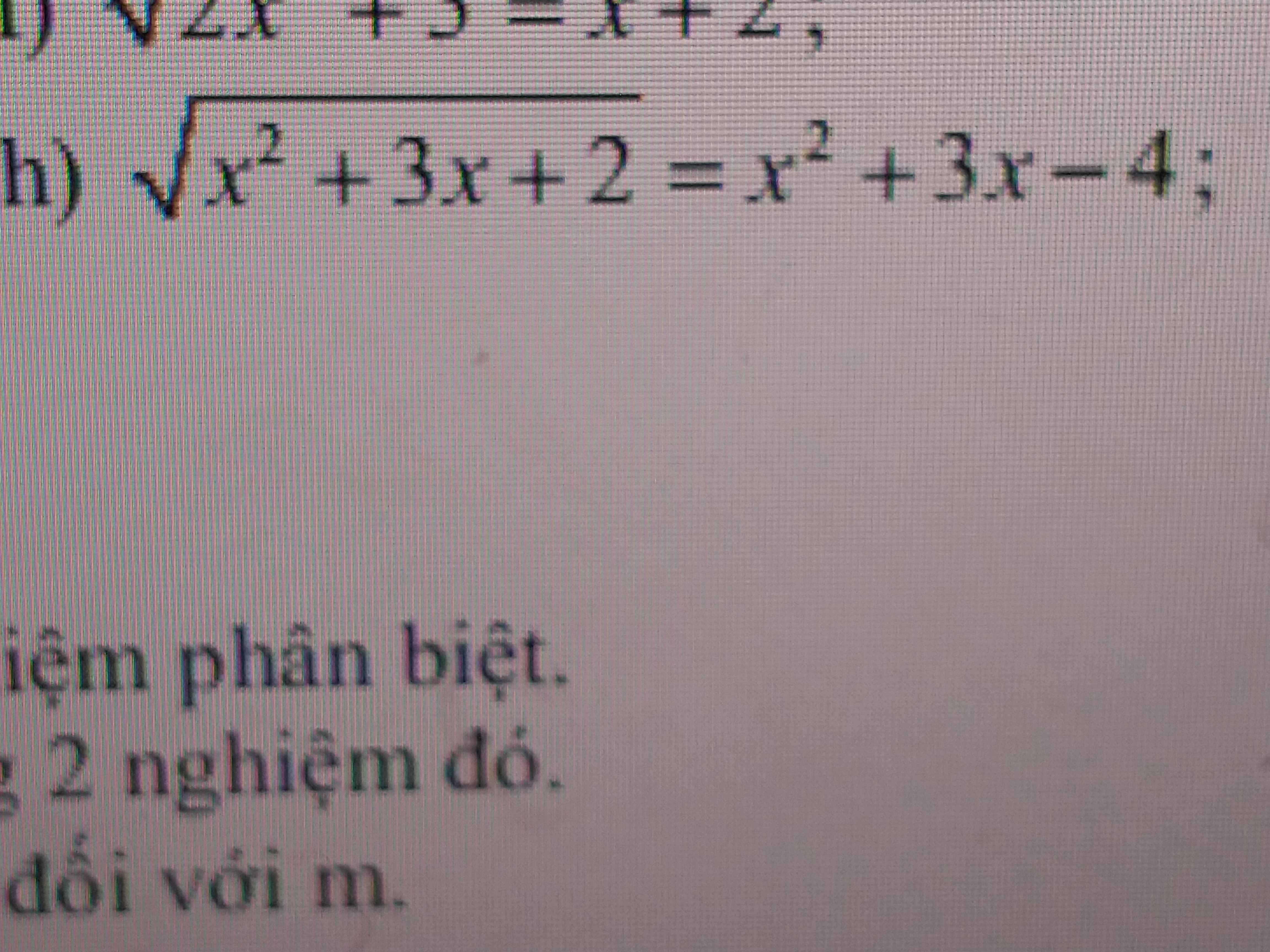
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 92:
\(a,PTHH:Zn+2HCl\to ZnCl_2+H_2\\ ZnO+2HCl\to ZnCl_2+H_2O\\ n_{H_2}=\dfrac{2,24}{22,4}=0,1(mol)\\ \Rightarrow n_{Zn}=0,1(mol)\\ \Rightarrow m_{Zn}=0,1.65=6,5(g)\\ \Rightarrow \%_{Zn}=\dfrac{6,5}{14,6}.100\%\approx44,52\%\\ \Rightarrow \%_{ZnO}=100\%-44,52\%=55,48\%\\ b,m_{ZnO}=14,6-6,5=8,1(g)\\ \Rightarrow n_{ZnO}=\dfrac{8,1}{81}=0,1(mol)\\ \Rightarrow \Sigma n_{HCl}=2n_{Zn}+2n_{ZnO}=0,4(mol)\\ \Rightarrow V_{dd_{HCl}}=\dfrac{0,4}{0,5}=0,8(mol)\)
Câu 93:
\(n_{H_2}=\dfrac{16,8}{22,4}=0,75(mol)\\ PTHH:Fe+H_2SO_4\to FeSO_4+H_2\\ \Rightarrow n_{Fe}=n_{H_2}=0,75(mol)\\ \Rightarrow m_{Fe}=0,75.56=42(g)\\ b,n_{H_2SO_4}=n_{H_2}=0,75(mol)\\ \Rightarrow C_{M_{H_2SO_4}}=\dfrac{0,75}{0,25}=3M\\ c,n_{FeSO_4}=0,75(mol)\\ \Rightarrow m_{CT_{FeSO_4}}=0,75.152=114(g)\\ V_{dd_{FeSO_4}}=V_{dd_{H_2SO_4}}=250(ml)\\ \Rightarrow m_{dd_{FeSO_4}}=250.1,1=275(g)\\ \Rightarrow C\%_{FeSO_4}=\dfrac{114}{275}.100\%\approx41,45\%\)
\(d,m_{FeSO_4.5H_2O}=242.0,75=181,5(g)\)

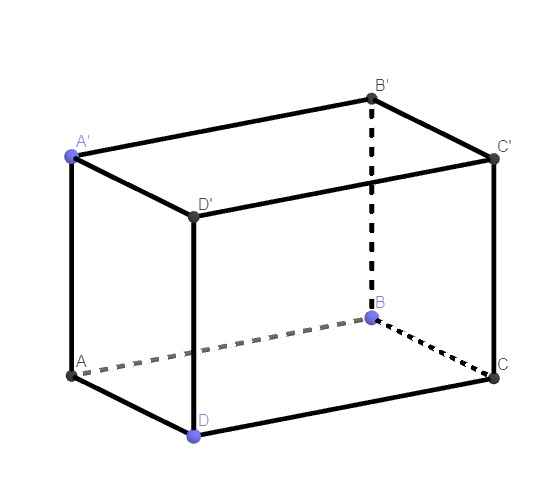
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)


Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng




nO2 = 5,6 : 22,4=0,25
pthh: 2KClO3 -t--> 2KCl + 3O2 (1)
0,16 <------------------------0,25(mol)
=> mKClO3 = 0,16.114,5=18,32(g)
nMg = 24:24=0,1 (mol)
pthh : 2Mg + O2 -t->2MgO
0,1------------>0,1(mol)
=> mMgO = 0,1.40= 4 (g))

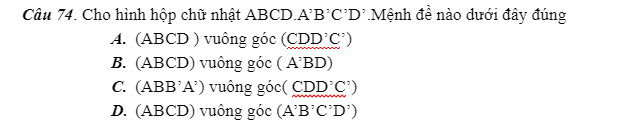
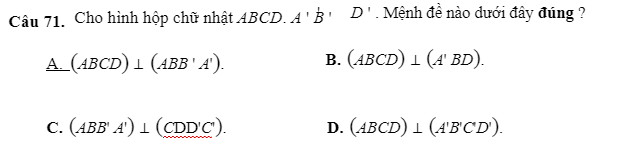







ĐKXĐ: \(\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
Đặt \(\sqrt{x^2+3x+2}=t\ge0\Rightarrow x^2+3x=t^2-2\)
Pt trở thành:
\(t=t^2-2-4\)
\(\Leftrightarrow t^2-t-6=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+3x+2}=3\)
\(\Leftrightarrow x^2+3x+2=9\)
\(\Leftrightarrow x^2+3x-7=0\) (bấm máy)
\(PT\Leftrightarrow\sqrt{x^2+3x+2}-3=x^2+3x-7\\ \Leftrightarrow\dfrac{x^2+3x-7}{\sqrt{x^2+3x+2}+3}-\left(x^2+3x-7\right)=0\\ \Leftrightarrow\left(x^2+3x-7\right)\left(\dfrac{1}{\sqrt{x^2+3x+2}+3}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+3x-7=0\\\sqrt{x^2+3x+2}+3=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3\pm\sqrt{37}}{2}\\\sqrt{x^2+3x+2}=-2\left(\text{vô nghiệm}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3+\sqrt{37}}{2}\\x=\dfrac{-3-\sqrt{37}}{2}\end{matrix}\right.\)
Thế vô PT ta thấy 2 nghiệm thỏa mãn
Vậy PT có nghiệm \(S=\left\{\dfrac{-3+\sqrt{37}}{2};\dfrac{-3-\sqrt{37}}{2}\right\}\)