Chọn A

Tập xác định

Ta có: 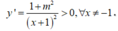 Suy ra hàm số y = x - m 2 x + 1 đồng biến trên 

Do đó: 

Theo giả thiết: 

* Hàm số đã cho liên tục trên R vì với 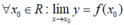 nên (1) đúng

* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.

* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x

Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1

nên hàm số không có GTLN.

* Phương trình x 2 - 2 | x | + 2 = 0  vô nghiệm nên đồ thị không cắt trục hoành.

f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )

Nên hàm số đã cho là hàm số chẵn.

Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.

Chọn B

Xét

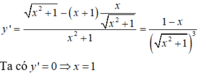
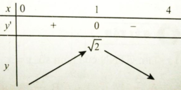
Ta có y' = 0 => x = 1

Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.

y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5

Ta có  ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1

Giá trị lớn nhất của hàm số   y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi

  m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3

Chọn B.

Đáp án B.

Phương pháp:    

Sử dụng cách vẽ đồ thị hàm số  y = f x  

Cách giải:

Xét hàm số  y = x 2 + 2 x + m − 4 = f x  có:

y ' = 2 x + 2  

y ' = 0 ⇔ x = − 1  

Bảng biến thiên:

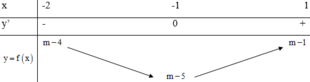
+)  m ≥ 5 :

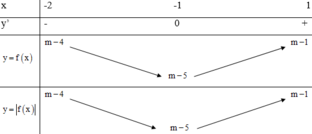
M a x − 2 ; 1 x 2 + 2 x + m − 4 = f 1 = m − 1 = 4 ⇒ m = 5  

(Thỏa mãn)

+) 4 ≤ m < 5 :

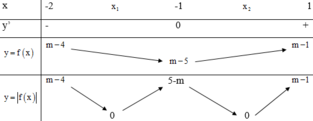
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x m − 1 ; 5 − m = 4  

Mà

m − 1 > 5 − m ,   ∀ m ∈ 4 ; 5 ⇒ m − 1 = 4 ⇒ m = 5

 (loại)

+) 1 ≤ m < 4 :  

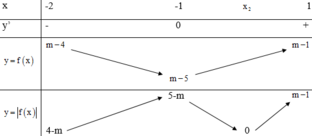
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x 5 − m ; m − 1 = 4.

m ∈ − 1 ; 3 ⇒ max y = 5 − m = 4 ⇔ m = 1    t m   

m ∈ − 1 ; 3 ⇒ max y = m − 1 = 4 ⇔ m = 5    k t m  

+) m < 1 :  

M a x − 2 ; 1 x 2 + 2 x + m − 4 = 5 − m = 4 ⇒ m = 1  

(Không thỏa mãn)

Vậy m ∈ 4 ; 1 ,  có hai giá trị của m thỏa mãn.