Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 9 cm, AC = 12 cm.
a) Tính BC, AH
b) Vẽ đường tròn tâm A bán kính AH. Từ C vẽ tiếp tuyến CD với đường tròn tâm A (D là tiếp điểm). Đường thẳng DH cắt AC tại I. Chứng minh \(IA\cdot IC=\dfrac{DH^2}{4}\)
c) Đường thẳng DA cắt đường tròn tâm A tại điểm thứ hai là E. Chứng minh BE là tiếp tuyến đường tròn tâm A.

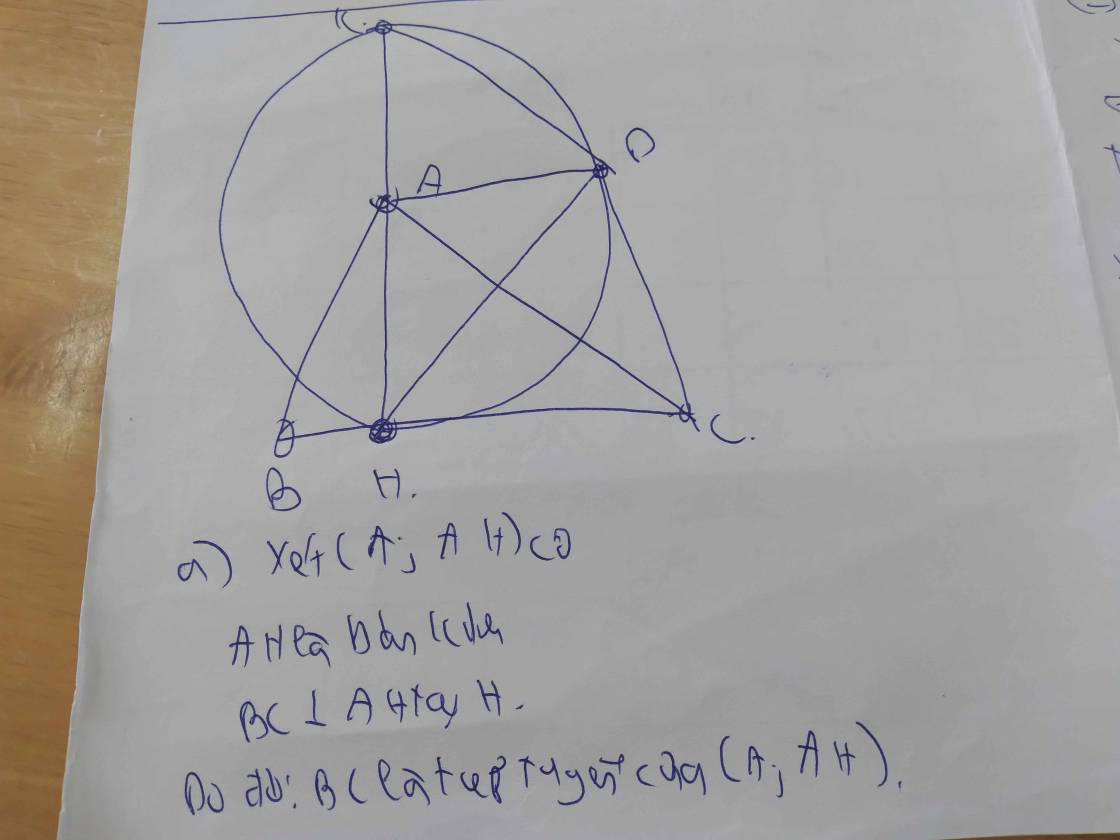


\(\left\{{}\begin{matrix}\widehat{DCA}=\widehat{HCA}\\\widehat{DCA}+\widehat{DAC}=90^0\\\widehat{HCA}+\widehat{HBA}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{HBA}=\widehat{DAC}\)
\(\left\{{}\begin{matrix}\widehat{DAC}+\widehat{BAE}=90^0\\\widehat{HBA}+\widehat{HAB}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{BAE}=\widehat{HAB}\)
Có \(\left\{{}\begin{matrix}AH=AE=R\\\widehat{BAE}=\widehat{HAB}\\\text{AB chung}\end{matrix}\right.\) \(\Rightarrow\Delta AHB=\Delta AEB\)
\(\Rightarrow\widehat{E}=\widehat{H}=90^0\Rightarrow BE\) là tiếp tuyến
Cách chứng minh ^BAE=^HAB khó nghĩ thật ạ.