Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


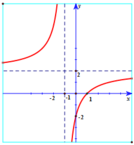
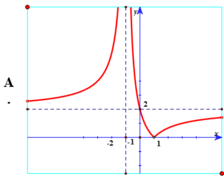
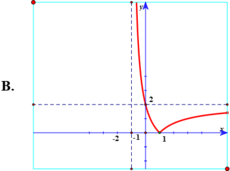
Chọn A.
Ta có:
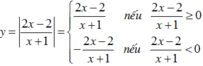
Đồ thị hàm số y = 2 x - 2 x + 1 có được bằng cách:
+ Giữ nguyên phần đồ thị hàm số y = 2 x - 2 x + 1 nằm phía trên trục hoành.
+ Lấy đối xứng phần đồ thị hàm số y = 2 x - 2 x + 1 nằm phía dưới trục hoành qua trục hoành.


Giải
a) y = f(x) = 3x
Cho x = 1 thì y = 3 .1 = 3 ; A(1;3)
b) y = f(x) = \(-\frac{1}{2}x\)
cho x = 2 thì y = 2 . \(-\frac{1}{2}\)= -1

Gọi A là giao điểm của đg thẳng y=2x+5 và trục Ox
Phương tình hoành độ giao điểm của y=2x+5 và trục Ox là:
0=2x+5 => x=-5/2
Vậy A(-5/2;0)

Điểm N thuộc đồ thị vì \(y_N=1=2\cdot x_N=2\cdot\dfrac{1}{2}\)
Điểm M ko thuộc đồ thị vì \(y_M=-4< >2\cdot x_M\)
Lời giải:
ĐTHS $y=2x$:
Muốn kiểm tra xem 1 điểm có thuộc đths không thì ta thay tung độ và hoành độ của đồ thị đó vào phương trình đồ thị đó xem có thỏa mãn không là được.
$x_M=1; y_M=-4$ nên $y_M\neq 2x_M$ nên $M$ không thuộc đths $y=2x$
$x_N=\frac{1}{2}; y_N=2$ nên $y_N=2x_N$ nên $N$ thuộc đths $y=2x$
y=2x
x=0=> y=0 => A(0;0)
x=1 => y=2 => B(1;2)
=> đồ thị y=2x đi qua A(0;0) và B(1;2)
cái kia làm tương tự