a) Để hàm số trên đồng biến thì a>0  <=> m+5>0  <=> m>-5

b) thay A(2;3) vào đồ thị hs ta đc 3=(m+5).2+2m-10  =>m=3/4

mình cần câu c, d 

a) Hàm số đồng biến `<=>m+1>0<=>m>-1`

b) `d_1` đi qua `A(1;2) <=> 2=(m+1).1+m-1<=>m=1`

c) `d_1 //// y=-1/3 x+1 <=>` \(\left\{{}\begin{matrix}m+1=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{4}{3}\\m\ne2\end{matrix}\right.\Leftrightarrow m=-\dfrac{4}{3}\)

a. \(\left\{{}\begin{matrix}DB:m+4>0\Leftrightarrow m>-4\\NB:m+4< 0\Leftrightarrow m< -4\end{matrix}\right.\)

\(a,\) Đồng biến \(\Leftrightarrow m+4>0\Leftrightarrow m>-4\)

Nghịch biến \(m+4< 0\Leftrightarrow m< -4\)

\(b,A\left(-1;2\right)\in\left(d\right)\Leftrightarrow-m-4-m+6=2\Leftrightarrow m=0\)

\(\Leftrightarrow y=4x+6\)

a, Hàm số ĐB\(\Leftrightarrow\) a \(>\)0

                       \(\Leftrightarrow\) m-2 \(>\)0  \(\Leftrightarrow\) m \(>\)2

Vậy m\(>\)2 thì hàm số ĐB.

b,ĐTHS (*) // vs đt y=2x-1 \(\Leftrightarrow\)\(\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\)

                                          \(\Leftrightarrow\)\(\hept{\begin{cases}m-2=2\\2m+1\ne-1\end{cases}}\)                   

                                           \(\Leftrightarrow\hept{\begin{cases}m=4\left(tm\right)\\m\ne-1\end{cases}}\)

Vậy m=4;m\(\neq\)-1 thì ĐTHS (*) // vs đt y=2x-1

c,Gọi A(\(x_0;y_0\)) là điểm cố định mà ĐTHS (*) luôn đi qua vs mọi m

   Thay x=\(x_0\) ,y=\(y_0\) vào pt đt (*) ta đc̣:

         \(y_0=\left(m-2\right)x_02m+1\)\(\Leftrightarrow\)\(mx_0-2x_0+2m+1-y_0=0\)

          \(\Leftrightarrow m\left(x_0+2\right)-2x_0+1-y_0=0\left(1\right)\)

Để đt (*) luôn đi qua A vs mọi m thì pt (1) luôn đúng vs mọi m ( pt (1) có vô số nghiệm m)

       Điều này xảy ra \(\Leftrightarrow\hept{\begin{cases}x_0+2=0\\-2x_0+1-y_0=0\end{cases}}\)                                                           

                                 \(\Leftrightarrow\hept{\begin{cases}x_0=-2\\y_0=5\end{cases}}\)                                                                                                                                                                        

                                 \(\Rightarrow A\left(-2;5\right)\)                                         

Vậy A(-2;5) là điểm cố định mà ĐTHS (*) luôn luôn đi qua vs mọi m

holle

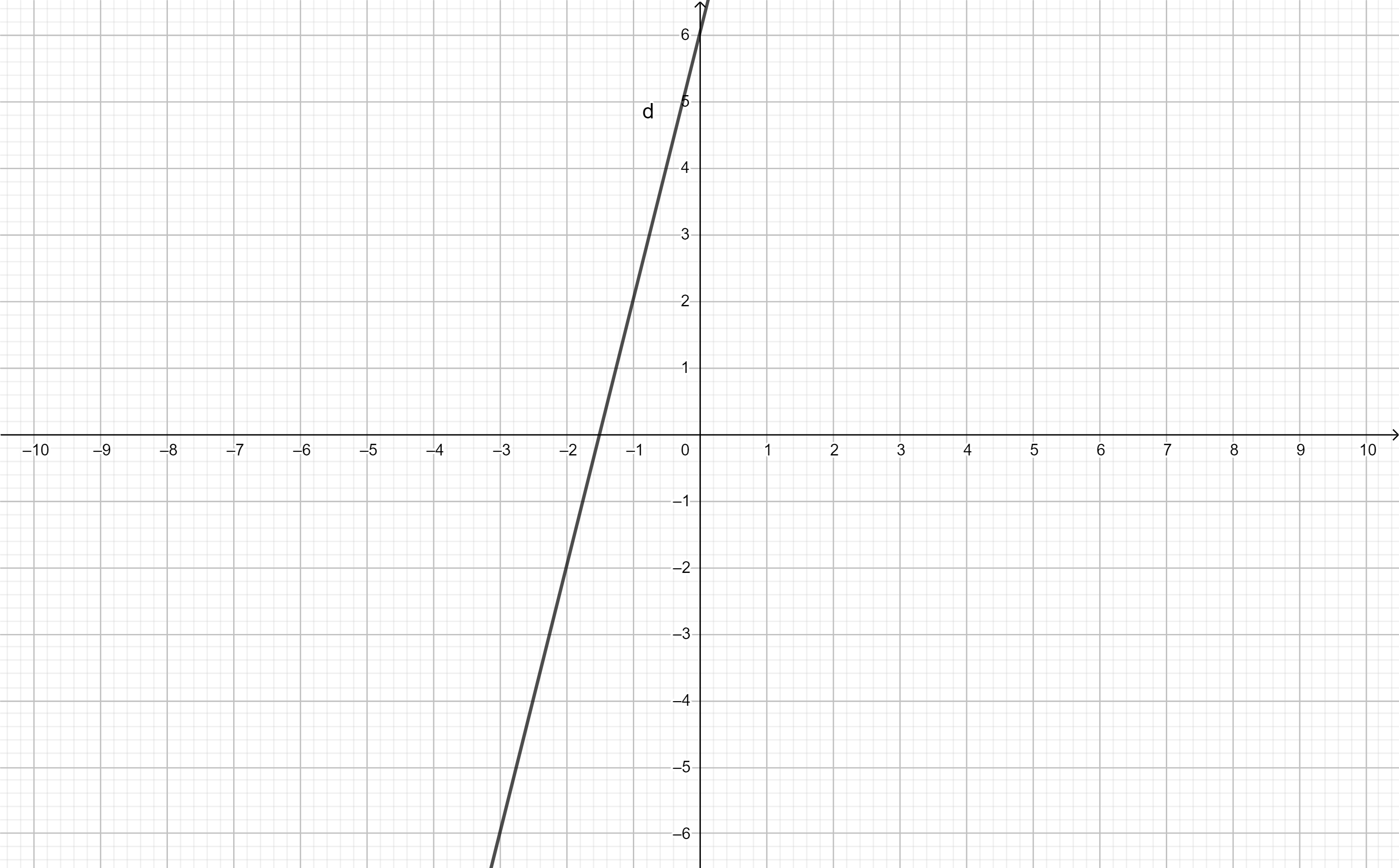
h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)

Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox

\(tan\alpha=a=1\)

=>\(\alpha=45^0\)

y=x+4

=>x-y+4=0

Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:

\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)

a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)

=>\(m\ne2\)

b: Để (1) đồng biến thì m-2>0

=>m>2

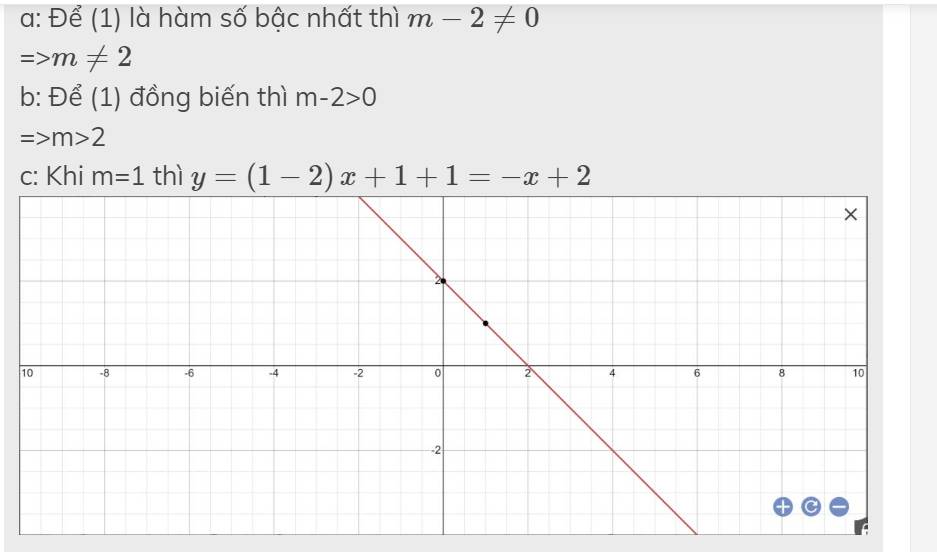
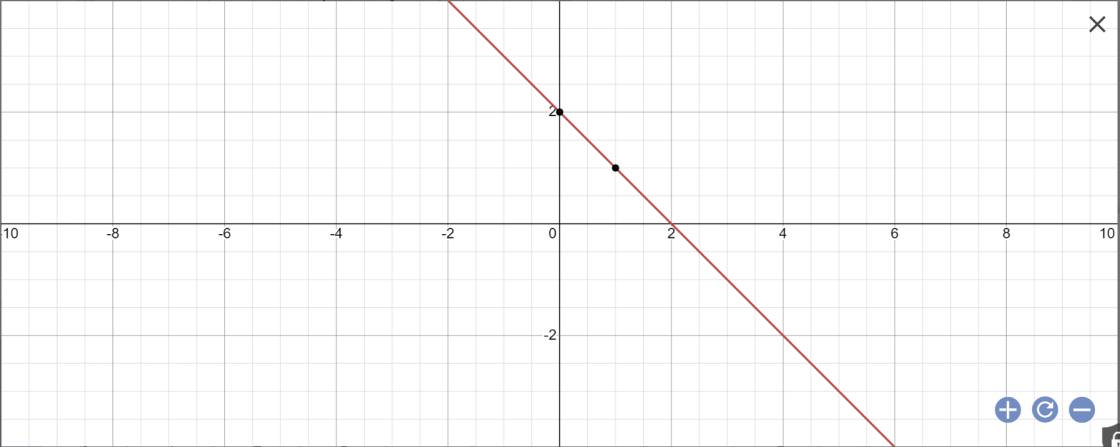
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)

d: Thay x=2 và y=1 vào (1), ta được:

\(2\left(m-2\right)+m+1=1\)

=>2m-4+m=0

=>3m-4=0

=>3m=4

=>\(m=\dfrac{4}{3}\)

e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)

=>m=3

f: Để (1) tạo với trục Ox một góc tù thì m-2<0

=>m<2

g: Thay x=0 vào y=5x+6, ta được:

\(y=5\cdot0+6=6\)

Thay x=0 và y=6 vào (1), ta được:

\(0\left(m-2\right)+m+1=6\)

=>m+1=6

=>m=5

Bài 1:

Đặt:  (d):  y = (m+5)x + 2m - 10

Để y là hàm số bậc nhất thì:  m + 5 # 0    <=>   m # -5

Để y là hàm số đồng biến thì: m + 5 > 0  <=>  m > -5

(d) đi qua A(2,3) nên ta có:

3 = (m+5).2 + 2m - 10

<=>  2m + 10 + 2m - 10 = 3

<=>  4m = 3

<=> m = 3/4

(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:

9 = (m+5).0 + 2m - 10

<=> 2m - 10 = 9

<=>  2m = 19

<=> m = 19/2

(d) đi qua điểm 10 trên trục hoành nên ta có:

0 = (m+5).10 + 2m - 10

<=> 10m + 50 + 2m - 10 = 0

<=>  12m = -40

<=> m = -10/3

(d) // y = 2x - 1  nên ta có:

\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\)   <=>   \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\)  <=>  \(m=-3\)

B1:

b) Để y là hàm số đồng biến thì m+5>0

hay m>-5

B1:

Đặt (d): y=(m+5)x+2m-10

c) Để đồ thị hàm số đi qua điểm A(2;3) thì

Thay x=2 và y=3 vào (d), ta được:

\(2\left(m+5\right)+2m-10=3\)

\(\Leftrightarrow2m+10+2m-10=3\)

\(\Leftrightarrow4m=3\)

hay \(m=\dfrac{3}{4}\)

a) H/s là bậc nhất ⇔ m+5≠0 ⇔m ≠-5

b)  H/s đồng biến ⇔ m+5> 0 ⇔ m> -5

c)  H/s đi qua A( 2,3)    ⇔  2=(m+5).2 +2m -10    ⇔ 2m+ 2m +10 -10 =2

                                     ⇔ m= \(\dfrac{1}{2}\)

d) H/s cắt trục tung tại điểm có tung độ bằng 9

⇔ x=0 thì y=9       ⇔ (m+5).0 +2m -10 =9

                             ⇔m= \(\dfrac{19}{2}\)

e) H/s đi qua điểm 10 trên trục hoành ⇔ y=0, x=10 

⇔ 0= (m+5).10 +2m -10      ⇔m= \(\dfrac{-40}{12}\)

f) h/s song song với y=2x-1 

⇔ \(\left\{{}\begin{matrix}m+5=2\\2m-10\ne-1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}m=-3\\m\ne\dfrac{9}{2}\end{matrix}\right.\)

⇔m=-3

thank you

a) Để hàm số y = (2m - 3)x - 1 // với đường thẳng y = -5x + 3 

<=> \(\hept{\begin{cases}2m-3=-5\\-1\ne3\end{cases}}\)<=> 2m = -2 <=> m = -1

b) Hàm số y = (2m - 3)x - 1 đi qua điểm A(-1; 0) => x = -1 và y = 0

Do đó: 0 = (2m - 3).(-1) - 1 = 0 <=> 3 - 2m = 1 <=> 2m = 2 <=> m = 1

Vậy để đò thị hàm số đi qua A(-1; 0) <=> m = 0

c) Gọi tọa độ gđ của 3 đường thẳng y = (2m- 3 )x - 1 , y = 1 và y = 2x - 5 là (x0; y0)

Do đó: \(\hept{\begin{cases}y_0=\left(2m-3\right)x_0-1\\y_0=1\\y_0=2x_0-5\end{cases}}\) <=> \(\hept{\begin{cases}1=\left(2m-3\right)x_0-1\\2x_0-5=1\end{cases}}\) 

<=> \(\hept{\begin{cases}\left(2m-3\right)x_0=2\\2x_0=6\end{cases}}\) <=> \(\hept{\begin{cases}\left(2m-3\right).3=2\\x_0=3\end{cases}}\) <=> 2m - 3 = 2/3 <=> 2m = 11/3 <=> m = 11/6

Vậy m = 11/6 thì đồ thị hàm số đã cho và các đường thẳng y = 0 và y = 2x - 5 đồng quy tại 1 điểm