cho x và y là các số thực ko âm x2+y2bé hơn bằng 2
tính giá trị biểu thức P=√x.(29x+3y) +√y.(29x+3y)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài là thế này đúng không bạn:
Cho các số thực không âm x; y thỏa mãn: \(x^2+y^2\le2\)
Tìm GTLN của: \(P=\sqrt{29x+3y}+\sqrt{3x+29y}\)
P/s: bạn nên sử dụng tính năng gõ công thức để người khác dễ đọc hơn (đây là tính năng rất đơn giản, dễ dàng làm quen, nó nằm ở biểu tượng \(\sum\) trên khung soạn thảo)

Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2\leq (x+y)[(29x+3y)+(29y+3x)]=32(x+y)^2\leq 32.(x^2+y^2)(1+1)=64(x^2+y^2)\leq 64.2=128$
$\Rightarrow P\leq 8\sqrt{2}$
Vậy $P_{\max}=8\sqrt{2}$

Áp dụng bất đẳng thức Cosi ta có:
1 32 32 x 29 x + 3 y ≤ 1 4 2 32 x + 29 x + 3 y 2 = 1 8 2 61 x + 3 y
Tương tự
1 32 32 y 29 y + 3 x ≤ 1 8 2 61 y + 3 x
=> P ≤ 4 2 x + y ≤ 4 2 x 2 + 1 2 + y 2 + 1 2 = 8 2
Vậy P min = 8 2 <=> x = y = 1

Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó ![]()
![]()
![]()
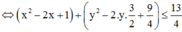
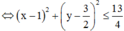
Xét biểu thức P, ta có 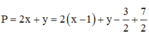
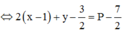
Áp dụng BĐT Bunhiacopxki, có 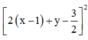
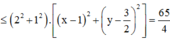
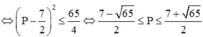
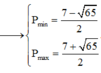
Tính giá trị hay tìm GTLN, GTNN bạn?