d: \(\Delta=m^2-2m+1-4m\left(m-1\right)=m^2-2m+1-4m^2+4m=-3m^2+2m+1\)

Để bất phương trình có nghiệm đúng với mọi x thì \(\left\{{}\begin{matrix}-3m^2+3m-m+1< 0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(-3m+1\right)< 0\\m< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(3m-1\right)>0\\m< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< \dfrac{1}{3}\end{matrix}\right.\\m< 0\end{matrix}\right.\Leftrightarrow m< 0\)

giải thêm phần f) đc ko bạn ?

3:

x^2-2x+1-m^2<=0

=>(x-1)^2-m^2<=0

=>(x-1)^2<=m^2

=>-m<=x-1<=m

=>-m+1<=x<=m+1

mà x thuộc [-1;2]

nên -m+1>=-1 và m+1<=2

=>-m>=-2 và m<=1

=>m<=2 và m<=1

=>m<=1

2.

b, \(-4< \dfrac{2x^2+mx-4}{-x^2+x-1}< 6\)

\(\Leftrightarrow\left\{{}\begin{matrix}-4< \dfrac{2x^2+mx-4}{-x^2+x-1}\left(1\right)\\\dfrac{2x^2+mx-4}{-x^2+x-1}< 6\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow4\left(x^2-x+1\right)>2x^2+mx-4\)

\(\Leftrightarrow2x^2-\left(m+4\right)x+8>0\)

Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2+8m-48< 0\Leftrightarrow-12< m< 4\)

\(\left(2\right)\Leftrightarrow-6\left(x^2-x+1\right)< 2x^2+mx-4\)

\(\Leftrightarrow8x^2+\left(m-6\right)x+2>0\)

Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2-12m-28< 0\Leftrightarrow-2< x< 14\)

Vậy \(m\in\left(-2;4\right)\)

2.

a, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-4\right)x^2+\left(1+m\right)x+2m-1>0\) có nghiệm đúng với mọi x

\(\Leftrightarrow\left\{{}\begin{matrix}m-4>0\\\Delta=m^2+2m+1-4\left(m-4\right)\left(2m-1\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>4\\\left[{}\begin{matrix}m< \dfrac{3}{7}\\m>5\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow m>5\)

Đặt 

Suy ra 

Ta có 

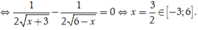
Ta có bảng biến thiên

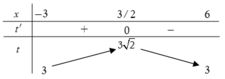
Từ bảng biến thiên ta suy ra 

Khi đó bất phương trình trở thành: 

Xét hàm số  với 

Ta có 

Suy ra hàm số f(t) nghịch biến trên 

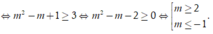
Chọn C.

1.

\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)

\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)

2.

\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)

Không tồn tại m thỏa mãn

a ơi giúp e với 

https://hoc24.vn/cau-hoi/tim-gtnn-cua-t2m4-2m2-12m-18.333959553188

a) bạn thay x=2 vao pt roi tim m;

4 -2(2m+3)+m² +3m+ 2 = 0

tim dc m roi bạn thay m vao pt da cho se tim dc x₂

_{b) denta luon >0 nen pt luon 2 nghiem k phu thuoc vao m}

a, Ta có:

\(\Delta=\left[-\left(m+5\right)\right]^2-4\left(2m+6\right)\\ =m^2+10m+25-8m-24\\ =m^2+2m+1\\ =\left(m+1\right)^2\ge0\)

Vậy pt luôn có 2 nghiệm x₁,x₂

b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=m+5\\x_1x_2=2m+6\end{matrix}\right.\)

\(x^2_1+x^2_2=13\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\\ \Leftrightarrow\left(m+5\right)^2-2\left(2m+6\right)=13\\ \Leftrightarrow m^2+10m+25-4m-12-13=0\\ \Leftrightarrow m^2+6m=0\\ \Leftrightarrow m\left(m+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-6\end{matrix}\right.\)

em cảm ơn ạ

Bạn cần viết đề bằng công thức toán ( biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.