Cho đường tròn (O) đường kính AB cố định. Từ điểm C bất kỳ trên đoạn OA vẽ dây MN vuông góc với AB. Lấy điểm D thuộc cung AM nhỏ; BD cắt MN tại E; AD cắt tia NM tại F. a) Chứng minh : tứ giác ADEC nội tiếp. b) Chứng minh: CA.CB = CE.CF c) Tia AE cắt đường tròn ngoại tiếp tam giác DEF tại điểm I. Chứng minh I nằm trên đường tròn O. d) Xác định vị trí của điểm C trên OA sao cho chu vi tam giác OCN lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì D là một điểm nằm trên cung AM nhỏ của (O) nên D∈(O)
Xét (O) có
ΔADB nội tiếp đường tròn(A,D,B∈(O))
AB là đường kính của (O)(gt)
Do đó: ΔADB vuông tại D(Định lí)
⇔\(\widehat{ADB}=90^0\)
hay \(\widehat{ADE}=90^0\)
Xét tứ giác ADEC có
\(\widehat{ADE}\) và \(\widehat{ACE}\) là hai góc đối
\(\widehat{ADE}+\widehat{ACE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)
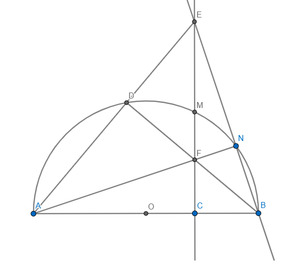

1) Vì AB là đường kính \(\Rightarrow\angle ADB=90\) mà \(\angle ECB=90\Rightarrow BCDE\) nội tiếp
2) Vì \(\left\{{}\begin{matrix}EF\bot AB\\AF\bot EB\end{matrix}\right.\Rightarrow F\) là trực tâm tam giác EAB \(\Rightarrow BF\bot AE\)
mà \(BD\bot AE\left(\angle BDA=90\right)\Rightarrow B,F,D\) thẳng hàng
Ta có: \(\angle FNB+\angle FCB=90+90=180\Rightarrow FNBC\) nội tiếp
Xét \(\Delta AFC\) và \(\Delta ABN:\) Ta có: \(\left\{{}\begin{matrix}\angle ACF=\angle ANB=90\\\angle NABchung\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta ABN\left(g-g\right)\Rightarrow\dfrac{AF}{AC}=\dfrac{AB}{AN}\Rightarrow AF.AN=AB.AC\)
Tương tự \(\Rightarrow BF.BD=BC.BA\)
\(\Rightarrow AF.AN+BF.BD=AB.AC+AB.BC=AB^2=4R^2\)
3) Gọi G là giao điểm của (AEF) và AB
Ta có: \(\angle FGB=\angle AEF\left(AEFGnt\right)=\angle DBA\left(BCDEnt\right)\Rightarrow\Delta GFB\) cân tại F có \(FC\bot GB\Rightarrow CB=CG\)
mà C,B cố định \(\Rightarrow G\) cố định
Vì AEFG nội tiếp \(\Rightarrow I\in\) trung trực AG mà A,G cố định \(\Rightarrow\) đpcm

a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm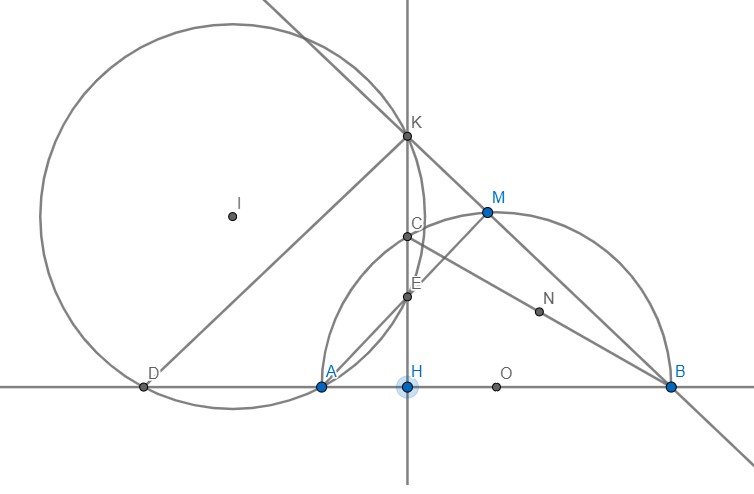

Gọi A' là giao điểm của đường tròn ngoại tiếp tam giác AEF và tia AB
Ta chứng minh được E,A,N và M, A, F thẳng hàng
=> A đối xứng với A' qua C => B đối xứng với A' qua điểm A mà A' cố định
=> Tâm I của đường tròn ngoại tiếp tam giác BMN nằm trên đường trung trực của đoạn thẳng BA'.
a) Vì điểm D thuộc cung AM nhỏ nên D nằm trên đường tròn(O)
Xét (O) có
\(\widehat{ADB}\) là góc nội tiếp chắn \(\stackrel\frown{AB}\)
\(\stackrel\frown{AB}\) là nửa đường tròn(AB là đường kính của (O))
Do đó: \(\widehat{ADB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{ADE}=90^0\)
Xét tứ giác ADEC có
\(\widehat{ADE}\) và \(\widehat{ACE}\) là hai góc đối
\(\widehat{ADE}+\widehat{ACE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)