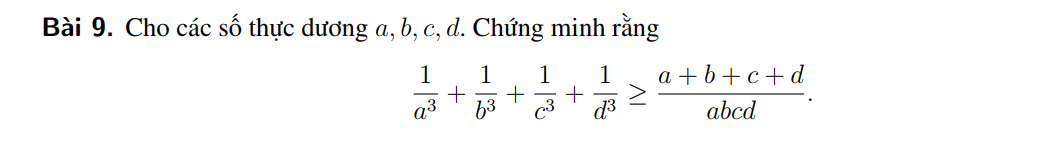Với n=0 \(\Rightarrow\) phương trình có 2 nghiệm duy nhất là \(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)

Với n \(\ne0\)

Để phương trình có nghiệm duy nhất \(\Leftrightarrow\dfrac{n}{2}\ne\dfrac{2}{n}\Rightarrow n^2\ne4\Rightarrow n\ne\pm2\)

Vậy hệ phương trình có nghiệm duy nhất \(\forall n\ne\pm2\)

cho mình hỏi có đúng với nghiệm nguyên không vì đề bài yêu cầu nghiệm nguyên ạ ?

Thực hiện lần lượt BĐT cô-si 3 số cho từng bộ 3 vế trái, ví dụ:

\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\ge3\sqrt[3]{\dfrac{1}{a^3b^3c^3}}=\dfrac{3}{abc}\)

Làm tương tự, sau đó cộng vế và quy đồng vế phải là sẽ được BĐT cần chứng minh

Lời giải:

ĐK:.............

Đặt $\sqrt{2x^2+x+6}=a; \sqrt{x^2+x+2}=b$ với $a,b\geq 0$ thì PT trở thành:

$a+b=\frac{a^2-b^2}{x}$

$\Leftrightarrow (a+b)(\frac{a-b}{x}-1)=0$

Nếu $a+b=0$ thì do $a,b\geq 0$ nên $a=b=0$

$\Leftrightarrow \sqrt{2x^2+x+6}=\sqrt{x^2+x+2}=0$ (vô lý)

Nếu $\frac{a-b}{x}-1=0$

$\Leftrightarrow a-b=x$

$\Leftrightarrow \sqrt{2x^2+x+6}=\sqrt{x^2+x+2}+x$

$\Rightarrow 2x^2+x+6=2x^2+x+2+2x\sqrt{x^2+x+2}$ (bình phương 2 vế)

$\Leftrightarrow 2=x\sqrt{x^2+x+2}(1)$

$\Rightarrow 4=x^2(x^2+x+2)$

$\Leftrightarrow x^4+x^3+2x^2-4=0$

$\Leftrightarrow (x-1)(x^3+2x^2+4x+4)=0$

Từ $(1)$ ta có $x>0$. Do đó $x^3+2x^2+4x+4>0$ nên $x-1=0$

$\Rightarrow x=1$Vậy..........

KO

a, - Thay m = 2 vào phương trình ta được :\(x+2\sqrt{x-1}-3=0\)

\(\Leftrightarrow2\sqrt{x-1}=3-x\)

\(\Leftrightarrow4\left(x-1\right)=x^2-6x+9\left(x\le3\right)\)

\(\Leftrightarrow4x-4=x^2-6x+9\)

\(\Leftrightarrow x^2-10x+13=0\)

\(\Leftrightarrow\)\(x=5\pm2\sqrt{3}\) ( TM  )

b, Ta có : \(x+2\sqrt{x-1}-m^2+6m-11=0\)

\(\Leftrightarrow x-1+2\sqrt{x-1}+1-m^2+6m-11=0\)

\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=m^2-6m+9+2=\left(m-3\right)^2+2\)

\(\Leftrightarrow\sqrt{x-1}-1=\pm\sqrt{\left(m-3\right)^2+2}\)

\(\Leftrightarrow\sqrt{x-1}=1\pm\sqrt{\left(m-3\right)^2+2}\)

\(\Leftrightarrow x=\left(1\pm\sqrt{\left(m-3\right)^2+2}\right)^2+1\ge1\) ( TM )

=> ĐPCM

a) Thay \(m=2\) vào phương trình

\(\Rightarrow x+2\sqrt{x-1}-3=0\)

\(\Leftrightarrow2\sqrt{x-1}=3-x\)   \(\left(3\ge x\ge1\right)\)

\(\Rightarrow4x-4=9-6x+x^2\)

\(\Leftrightarrow x^2-10x+13=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=5+2\sqrt{3}\left(loại\right)\\x=5-2\sqrt{3}\end{matrix}\right.\)

  Vậy ...

b) Đặt \(\sqrt{x-1}=a\)  \(\left(a\ge0\right)\)

\(\Rightarrow a^2+2a-m^2+6m-10=0\)

Ta có: \(\Delta'=m^2-6m+11\ge0\forall m\)

  Vậy phương trình luôn có nghiệm với mọi m

Ta có: \(\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left[\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]}\) 

Lại có: \(4\sqrt{x}\ge0\) với mọi x

\(3\left[\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]>0\) với mọi x

\(\Rightarrow\) \(\dfrac{4\sqrt{x}}{3\left[\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]}\ge0\) với mọi x

Dấu "=" xảy ra \(\Leftrightarrow\) x = 0

Vậy ...

Chúc bn học tốt! (Mk ms nghĩ ra được GTNN thôi thông cảm!)

Còn tìm GTLN:

Ta có: \(\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left[\left(\sqrt{x}-1\right)^2+\sqrt{x}\right]}\le\dfrac{4\sqrt{x}}{3\sqrt{x}}=\dfrac{4}{3}\)

Dấu "=" xảy ra \(\Leftrightarrow\) \(\sqrt{x}-1=0\) \(\Leftrightarrow\) x = 1

Vậy ...

Chúc bn học tốt!

CÁc số tròn chục nhỏ hơn 90 là :

10 ; 20 ; 30 ; 40 ; 50 ; 60 ; 70 ; 80

Tổng của các số tròn chục nhỏ hơn 90 là :

10 + 20 + ... + 80 = ( 80 + 10 ) x 8 : 2

= 90 x 8 : 2 = 720 : 2 = 360

Ta có bài toán quen thuộc sau: 

Nếu \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\) thì \(x+y=0\)

Do đó từ giả thiết ta chỉ cần chứng minh được \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\) thì bài toán được giải quyết.

Đặt \(\left\{{}\begin{matrix}x+\sqrt{x^2+1}=a>0\\y+\sqrt{y^2+1}=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{x^2+1}=a-x\\\sqrt{y^2+1}=b-y\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x^2+1=a^2+x^2-2ax\\y^2+1=b^2+y^2-2by\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2ax=a^2-1\\2by=b^2-1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{a^2-1}{2a}\\y=\dfrac{b^2-1}{2b}\end{matrix}\right.\)

Thế vào giả thiết:

\(\left(\dfrac{a^2-1}{2a}+\sqrt{1+\left(\dfrac{b^2-1}{2b}\right)^2}\right)\left(\dfrac{b^2-1}{2b}+\sqrt{1+\left(\dfrac{a^2-1}{2a}\right)^2}\right)=1\)

\(\Leftrightarrow\left(\dfrac{a^2-1}{2a}+\sqrt{\dfrac{\left(b^2+1\right)^2}{\left(2b\right)^2}}\right)\left(\dfrac{b^2-1}{2b}+\sqrt{\dfrac{\left(a^2+1\right)^2}{\left(2a\right)^2}}\right)=1\)

\(\Leftrightarrow\left(\dfrac{a+b}{2}+\dfrac{a-b}{2ab}\right)\left(\dfrac{a+b}{2}-\dfrac{a-b}{2ab}\right)=1\) 

\(\Leftrightarrow\left(\dfrac{a+b}{2}\right)^2-\left(\dfrac{a-b}{2ab}\right)^2=1\) (1)

Chú ý rằng: \(1=\dfrac{4ab}{4ab}=\dfrac{\left(a+b\right)^2-\left(a-b\right)^2}{4ab}\)

Do đó (1) tương đương:

\(\left(\dfrac{a+b}{2}\right)^2-\dfrac{\left(a-b\right)^2}{\left(2ab\right)^2}=\dfrac{\left(a+b\right)^2}{4ab}-\dfrac{\left(a-b\right)^2}{4ab}\)

\(\Leftrightarrow\dfrac{\left(a+b\right)^2}{4}\left(1-\dfrac{1}{ab}\right)+\dfrac{\left(a-b\right)^2}{4ab}\left(1-\dfrac{1}{ab}\right)=0\)

\(\Leftrightarrow\left[\dfrac{\left(a+b\right)^2}{4}+\dfrac{\left(a-b\right)^2}{4ab}\right]\left(1-\dfrac{1}{ab}\right)=0\)

Do \(a;b>0\Rightarrow\dfrac{\left(a+b\right)^2}{4}+\dfrac{\left(a-b\right)^2}{4ab}>0\)

\(\Rightarrow1-\dfrac{1}{ab}=0\Leftrightarrow ab=1\)

Hay \(\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1\)

\(\Rightarrow x+y=0\Rightarrow P=100\)

\(n_{CO_2}=\dfrac{17.6}{44}=0.4\left(mol\right)\)

\(n_{H_2O}=\dfrac{10.8}{18}=0.6\left(mol\right)\)

\(m_O=m_A-m_C-m_H=6-0.4\cdot12-0.6\cdot2=0\)

\(\text{A chứa : C và H}\)

\(CT:C_xH_y\)

\(x:y=0.4:1.2=1:3\)

\(CTnguyên:\left(CH_3\right)_n\)

\(M_A=15\cdot2=30\left(g\text{/}mol\right)\)

\(\Leftrightarrow15n=30\)

\(\Leftrightarrow n=2\)

\(CT:C_2H_6\)

\(\)

x:y=0.4:1.2 là sao vậy anh