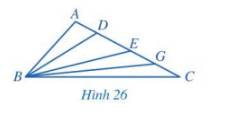
Cho tam giác ABC có góc A tù, trên cạnh AC lần lượt lấy điểm D, E, F sao cho D nằm giữa A và E; E nằm giữa D và F; F nằm giữa E và C. So sánh các đoạn thẳng BA, BD, BE, BF, BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác BAD:
+ Góc A tù (góc > 90°) nên cạnh BD là cạnh lớn nhất trong tam giác này (đối diện với góc A).
Nên BD > BA.
+ Góc A tù nên góc ABD và góc ADB là góc nhọn → góc BDE là góc tù (ba điểm A, D, E thẳng hàng hay góc ADE =180°). Vậy BE (đối diện với góc BDE) > BD.
Tương tự, ta có:
+ Góc BDE là góc tù nên góc DBE và góc DEB là góc nhọn → góc BEG là góc tù. Vậy BG > BE.
+ Góc BEG là góc tù nên góc EBG và góc EGB là góc nhọn → góc BGC là góc tù. Vậy BC > BG.
Vậy BA < BD <BE < BG < BC.
Hay các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự tăng dần là: BA, BD, BE, BG, BC.

DA*DP=DB*DC
=>DA/DC=DB/DP
=>ΔDAB đồng dạng với ΔDCP
=>góc BAD=góc PCD
=>ABPC nội tiếp

a: BC=căn 15^2+20^2=25cm
EC=25-5=20cm
ED//AC
=>BD/DA=BE/EC=1/4
=>BD/1=DA/4=15/5=3
=>BD=3cm; DA=12cm
EF//AB
=>FC/FA=EC/EB=4
=>FC/4=FA/1=20/5=4
=>FC=16cm; FA=4cm
b: DE=căn 5^2-3^2=4cm
=>C BDE=3+4+5=12cm
C CEF/C CAB=CE/CB=20/25=4/5
=>C CEF=4/5*(15+20+25)=4/5*60=48cm

Xét \(\Delta ABD\)có \(\widehat{A}\)tù \(\Rightarrow BA< BD\)(1); \(\widehat{ADB}< 90^o\)
\(\Rightarrow\widehat{BDE}>90^o\)\(\Rightarrow\Delta BDE\)tù tại D \(\Rightarrow BD< BE\)(2); \(\widehat{BED}< 90^o\)
\(\Rightarrow\widehat{BEC}>90^o\)\(\Rightarrow\Delta BEC\)tù tại E \(\Rightarrow BE< BC\)(3)
Từ (1), (2), (3) \(\Rightarrow BA< BD< BE< BC\left(đpcm\right)\)

Giải thích các bước giải:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=1800−FBC21800−FBC2 (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=1800−ABE21800−ABE2 (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)

a: Xét ΔHBE vuông tại H và ΔFEB vuông tại F có
BE chung
góc HEB=góc FBE
=>ΔHBE=ΔFEB
b: EF+EG
= BH+HD=BD

a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K