Cho tam giác MNP vuông tại M, có E là trung điểm của cạnh NP, gọi K là điểm đối xứng của M qua E. Tứgiác MNKP là hình gì? Vì sao? help mình vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác MNKP có
E là trung điểm của NP
E là trung điểm của MK
Do đó: MNKP là hình bình hành
mà \(\widehat{PMN}=90^0\)
nên MNKP là hình chữ nhật

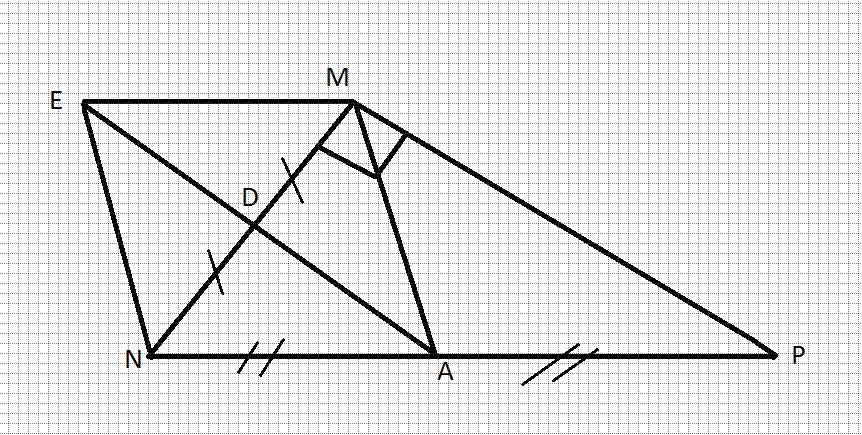
a: Xét ΔMNP có NA/NP=ND/NM
nên DA//MP
=>DA vuông góc với NM
=>EA vuông góc với NM
mà EA cắt NM tại trung điểm của EA
nên E đối xứng A qua MN
b: Xét tứ giác MENA có
D là trung điểm chung của MN và EA
AN=AM
Do đó: MENA là hình thoi

a: Xét tứ giác MPNI có
Q là trung điểm chung của MN và PI
Do đó: MPNI là hình bình hành
b: Xét ΔNMP có NQ/NM=NK/NP
nên QK//MP
=>QK vuông góc với MN

b: Xét tứ giác AMHI có
AM//HI
HM//AI
Do đó: AMHI là hình bình hành
mà \(\widehat{MAI}=90^0\)
nên AMHI là hình chữ nhật
Suy ra: AH=MI

a: Xét tứ giác AHDE có
I là trung điểm của AD
I là trung điểm của HE
Do đó: AHDE là hình bình hành
mà AD⊥HE
nên AHDE là hình thoi