Bài 1.Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:
a) AC P EF. b) Điểm E đối xứng với điểm F qua điểm B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 8 2016
AE = AD; AD = BC nên AE = BC(1)
DC = AB; DC = CF nên AB = CF (2)
GÓC EAB = BCF (Đồng vị) (3)
Từ (1); (2); (3) -> tgiac EAB = BCF (cgc) -> EB = BF (*)
Mặt khác: GÓC EBA = EFD (đồng vị); ABC = ADC (gt); CBF = AEB (đồng vị)
Cộng vế với vế: EBA + ABC + CBF = EFD + ADC + AEB
Mà EFD + ADC + AEB = 180 độ -> EBA + ABC + CBF = 180 độ (**)
Từ (*); (**) suy ra điểm E đối xứng với điểm F qua điểm B
CM
18 tháng 5 2017
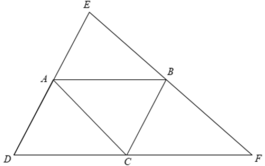
E là điểm đối xứng với D qua A ⇒ A là trung điểm của DE.
F là điểm đối xứng với D qua C ⇒ C là trung điểm của DF.
Xét Δ DEF có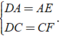
⇒ AC là đường trung bình của Δ DEF.
⇒ AC // EF
CM
22 tháng 9 2017
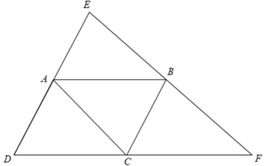
AC là đường trung bình của tam giác Δ DEF
⇒ AC = 1/2EF
+ ABCD là hình bình hành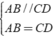
Mà DC = CF ⇒ AB = 1/2DF.
⇒ AB là đường trung bình của Δ DEF
Do đó B là trung điểm của EF hay E đối xứng với F qua B.
CM
16 tháng 4 2019
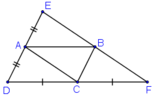
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
28 tháng 6 2021
Giải :
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
21 tháng 4 2017
Bài giải:
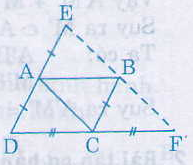
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.
CM
6 tháng 7 2017
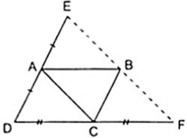
Theo giả thiết ta có:
+ A là trung điểm của DE thì AD = AE ( 1 )
+ C là trung điểm của DF thì CD = CF ( 2 )
Ta có ABCD là hình bình hành nên AD//BC
⇒ AE//BC ( 3 ) và AD = BC ( 4 )
Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )
Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được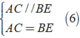 
Chứng minh tương tự, tứ giác ACBF là hình bình hành
Ta được: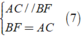
Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.
10 tháng 8 2016
AE = AD; AD = BC nên AE = BC(1)
DC = AB; DC = CF nên AB = CF (2)
GÓC EAB = BCF (Đồng vị) (3)
Từ (1); (2); (3) -> tgiac EAB = BCF (cgc) -> EB = BF (*)
Mặt khác: GÓC EBA = EFD (đồng vị); ABC = ADC (gt); CBF = AEB (đồng vị)
Cộng vế với vế: EBA + ABC + CBF = EFD + ADC + AEB
Mà EFD + ADC + AEB = 180 độ -> EBA + ABC + CBF = 180 độ (**)
Từ (*); (**) suy ra điểm E đối xứng với điểm F qua điểm B.