a) Quan sát đồ thị:

điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.

điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.

điểm (0;0) không thuộc đồ thị hàm số.

b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) =  - 1\)

Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)

c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

a: ĐKXĐ: \(\left\{{}\begin{matrix}-2< =x< =2\\x< >0\end{matrix}\right.\)

c: \(f\left(-x\right)=\dfrac{\sqrt{2-\left(-x\right)}-\sqrt{2+\left(-x\right)}}{-x}=\dfrac{\sqrt{2+x}-\sqrt{2-x}}{-x}=\dfrac{\sqrt{2-x}-\sqrt{2+x}}{x}=f\left(x\right)\)

Chọn A

a)

\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)

\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)

Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).

\( \Rightarrow {x_1} - {x_2} < 0\)

\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)

Ta có:

\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)

=> Hàm số nghịch biến trên (-2;-1)

Vậy hàm số giảm khi x tăng từ -2 đến -1

b)

\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)

Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).

\( \Rightarrow {x_1} - {x_2} < 0\)

\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)

Ta có:

\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)

=> Hàm số đồng biến trên (1;2)

Vậy hàm số tăng khi x tăng từ 1 đến 2.

a)

- Với \(x =  - 2 \Rightarrow f\left( { - 2} \right) =  - 2;g\left( { - 2} \right) =  - 2 + 3 = 1\);

- Với \(x =  - 1 \Rightarrow f\left( { - 1} \right) =  - 1;g\left( { - 1} \right) =  - 1 + 3 = 2\);

- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);

- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);

- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\); 

Ta có bảng sau:

b)

- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)

Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)

Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).

- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).

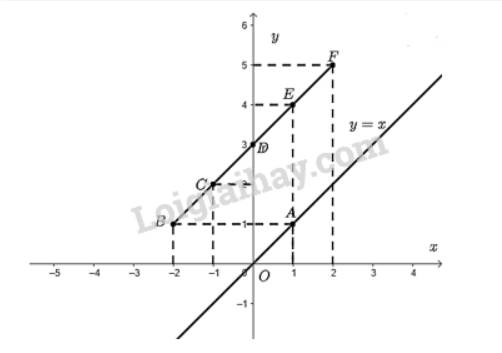
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.

Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):

Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).

Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).

Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).

a) Thay \({x_1} =  - 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:

\({y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)

\({y_2} = f\left( 1 \right) = {1^2} = 1\)

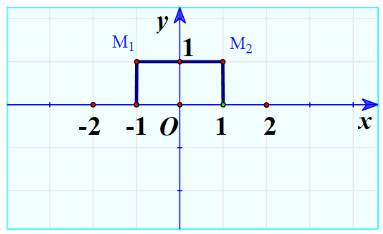
b) Ta có \({x_1} =  - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)\)

Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)

Biểu diễn trên mặt phẳng: