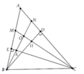
Cho ∆ABC có góc A =60°.Vẽ tia phân giác góc B,C cắt nhau tại O và lần lượt cắt AC tại M, AB tại N. CM BN+CM=BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


dau bai chac dung roi nhung qua la kho that to nghi mai k ra

+ ΔABC có Aˆ+ABCˆ+ACBˆ=180o. hay 60o+ABCˆ+ACBˆ=180o→ABCˆ+ACBˆ=120o
→ABCˆ+ACBˆ2=60o=ABCˆ2+ACBˆ2=B1ˆ+C1ˆ
+ Gọi CN∩BM=G
+ Δ có B1ˆ+C1ˆ+BGCˆ=180o. Hay 60o+BGCˆ=180o→BGCˆ=120o
+ Gọi GD là tia phân giác BGCˆ→G2ˆ=G3ˆ=60o
+ Tính G1ˆ=G4ˆ=G2ˆ=G3ˆ=60o
+ CM ΔNGB=ΔDGB (gcg) →BN=DB (2 cạnh tương ứng)
+CM ΔMGC=ΔDGC(gcg) →CM=CD (2 cạnh tương ứng)
+ Ta có BC=BD+CD=BN+CM (đpcm)
Nguồn: Chôm

Bài 1:
+ ΔABC có Aˆ+ABCˆ+ACBˆ=180o. hay 60o+ABCˆ+ACBˆ=180o→ABCˆ+ACBˆ=120o
→ABCˆ+ACBˆ2=60o=ABCˆ2+ACBˆ2=B1ˆ+C1ˆ
+ Gọi CN∩BM=G
+ Δ có B1ˆ+C1ˆ+BGCˆ=180o. Hay 60o+BGCˆ=180o→BGCˆ=120o
+ Gọi GD là tia phân giác BGCˆ→G2ˆ=G3ˆ=60o
+ Tính G1ˆ=G4ˆ=G2ˆ=G3ˆ=60o
+ CM ΔNGB=ΔDGB (gcg) →BN=DB (2 cạnh tương ứng)
+CM ΔMGC=ΔDGC(gcg) →CM=CD (2 cạnh tương ứng)
+ Ta có BC=BD+CD=BN+CM (đpcm)

a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.

a.Ta có:
ˆBID=12ˆBIC=12(180o−ˆBCI−ˆIBC)=12(180o−12ˆBCA−12ˆABC)=12(180o−12(ˆBCA+ˆABC)=12(180o−12(180o−ˆBAC)=60oBID^=12BIC^=12(180o−BCI^−IBC^)=12(180o−12BCA^−12ABC^)=12(180o−12(BCA^+ABC^)=12(180o−12(180o−BAC^)=60o
Lại có :
ˆNIB=ˆIBC+ˆICB
=1/2ˆABC+1/2ˆACB
=1/2(ˆABC+ˆACB)
=1/2(180o−ˆBAC)=60o
NIB^=IBC^+ICB^
=1/2ABC^+1/2ACB^
=1/2(ABC^+ACB^
=1/2(180o−BAC^)=60o
=>ˆNIB=ˆBID
=>ΔNIB=ΔDIB(g.c.g)
=>BN=BD(cmt)
b.Chứng minh tương tự câu a
→CD=CM
→BN+CM=BD+CD=BC→đpcm