Áp suất lớn nhất khi diện tích bị ép nhỏ nhất.

\(\Rightarrow S_{min}=6\cdot5=30cm^2=3\cdot10^{-3}m^2\)

\(F=p\cdot S=480\cdot3\cdot10^{-3}=1,44N\)

Trọng lượng vật chính là lực mà vật ép lên.

\(\Rightarrow P=F=1,44N\)

\(\Rightarrow P=10m\Rightarrow m=\dfrac{P}{10}=\dfrac{1,44}{10}=0,144kg=144g\)

Trọng lượng của vật là :

P = 10m = 10 * 0,84 = 8,4 (N)

Trong trường hợp này thì trọng lượng của vật chính là áp lực mà vật tác dụng lên mặt đất => P = F

Áp dụng công thức p = F/s

=> Để vật tạo ra áp suất lớn nhất thì s nhỏ nhất

Mà s nhỏ nhất là 5 * 6 = 30 (cm²) hay 0,003 m²

Vậy áp suất lớn nhất mà vật có thể tác dụng lên mặt đất là :

p = F/s = 8,4 : 0,003 = 2800 (pa)

Đáp số : 2800 Pa

áp dụng ct: \(p=\dfrac{F}{S}=>\left\{{}\begin{matrix}S1=\dfrac{10m}{p1}\\S2=\dfrac{10m}{p2}\\S3=\dfrac{10m}{p3}\end{matrix}\right.\)\(=>\left\{{}\begin{matrix}S1=\dfrac{20}{1000}=\dfrac{1}{50}m^2\\S2=\dfrac{20}{2000}=\dfrac{1}{100}m^2\\S3=\dfrac{20}{4000}=\dfrac{1}{200}m^2\end{matrix}\right.\)

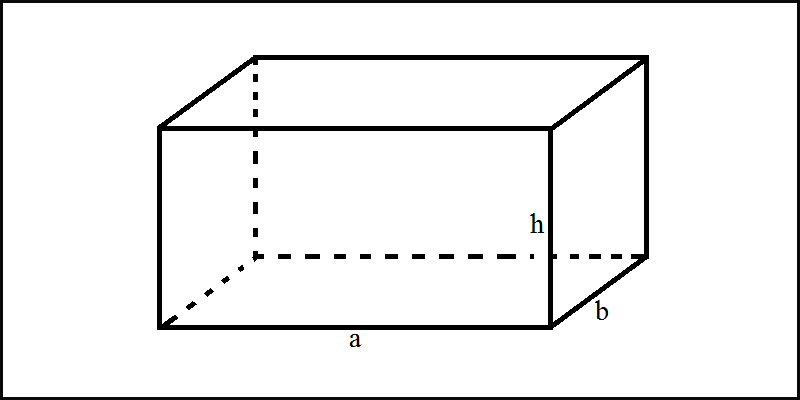
theo hình vẽ \(=>\left\{{}\begin{matrix}a.h=\dfrac{1}{50}\\a.b=\dfrac{1}{100}\\b.h=\dfrac{1}{200}\end{matrix}\right.\)(coi a>h>b)\(=>h=\dfrac{1}{50a},b=\dfrac{1}{100a}=>\dfrac{1}{5000a^2}=\dfrac{1}{200}=>a=0,2m=>h=0,1m,\)

\(=>b=0,05m\)

vậy kích thước: 0,2mx0,1mx0,05m

a) Áp lực của thùng gỗ :

\(F=m.10=5.10=50\left(N\right)\)

Áp suất tác dụng lên sàn nhà :

\(p=\dfrac{F}{S}=\dfrac{50}{1.10^{-3}}=50000\left(\dfrac{N}{m^2}\right)\)

b) Áp suất thùng gỗ sau khi lật ;

\(p'=\dfrac{F}{S'}=\dfrac{50}{2.10^{-3}}=25000\left(\dfrac{N}{m^2}\right)\)

làm sao để ra 1.10^-3 với 2.10^-3 vậy bạn

14cm

14cm

Áp lực do vật đó tác dụng lên mặt sàn trong cả 3 trường hợp đều là :

P = 10m = 10. 0,84 = 84 (N)

Áp suất do vật đó tác dụng lên mặt sau trong :
- Trường hợp 1 : \(p_1=\frac{P}{S_1}=\frac{84}{5,6}=2,8\left(pa\right)\)
- Trường hợp 2 :
- Trường hợp 3 :

kết quả là 2000N/m²