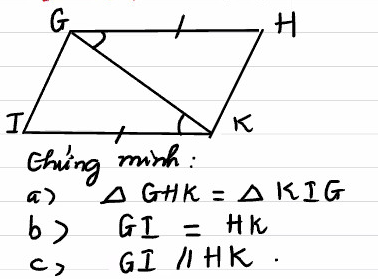
giúp mk câu c với ạ , cảm mơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 send - will receive
2 do - will improve
3 find - will give
4 will go - has
5 will go- gets
6 doesn't phone - will leave
7 don't study - won't pass
8 rains - won't have to
9 won't be able - watch
10 can't move - isn't
11 study - will pass


a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>AH=6(cm)
BC=BH+CH
=4+9
=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\\AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(tanABC=\dfrac{AC}{AB}=\dfrac{3}{2}\)
nên \(\widehat{ABC}\simeq56^0\)
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
\(AE\cdot AB+AF\cdot AC=AH^2+AH^2=2AH^2=2FE^2\)

1. PTBĐ chính: Thuyết minh
Vì văn bản bàn luận đến một vấn đề trong đời sống con người.
2. Vấn đề: Giải quyết vấn đề cho trẻ em nghèo.
Tác giả đưa vào đoạn trích những con số cụ thể để người đọc hiểu rằng kinh phí cho các vấn đề thực phẩm, y tế, giáo dục... rẻ hơn rất nhiều lần giá của các loại vũ khí, tên lửa... trong khi chúng chưa chắc đã được sử dụng vào mục đích chính đáng.
3. Em nêu ra một vài ý:
Phê phán chiến tranh, bạo lực...
Cố gắng giữ gìn hòa bình trên mọi phương diện
Cố gắng học tập, rèn luyện để phát triển đất nước...

1.
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{1}{2}\Rightarrow\widehat{A}=60^o\)
\(S=\dfrac{1}{2}bc.sinA=\dfrac{1}{2}.8.5.sin60^o=10\sqrt{3}\)
\(S=\dfrac{1}{2}a.h_a=\dfrac{1}{2}.7.h_a=10\sqrt{3}\Rightarrow h_a=\dfrac{20\sqrt{3}}{7}\)
\(2R=\dfrac{a}{sinA}=\dfrac{7}{\dfrac{\sqrt{3}}{2}}=\dfrac{14\sqrt{3}}{3}\Rightarrow R=\dfrac{7\sqrt{3}}{3}\)
\(S=pr=\dfrac{a+b+c}{2}.r=10r=10\sqrt{3}\Rightarrow r=\sqrt{3}\)
\(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{129}{4}\Rightarrow m_a=\dfrac{\sqrt{129}}{2}\)
6.
a, Công thức trung tuyến:
\(AM^2=c^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{2b^2+2c^2-a^2}{4}\Rightarrow a^2=2\left(b^2-c^2\right)\)
b, \(a^2=2\left(b^2-c^2\right)\Rightarrow\dfrac{2\left(b^2-c^2\right)}{a^2}=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}-\dfrac{c^2}{a^2}\right)=1\)
\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}.sin^2A-\dfrac{c^2}{a^2}.sin^2A\right)=sin^2A\)
\(\Leftrightarrow2\left(sin^2B-sin^2C\right)=sin^2A\)
Hay \(sin^2A=2\left(sin^2B-sin^2C\right)\)


Bài 3:
b: \(B_1=-\left|2x-3\right|+2\le2\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(B_2=-\left|x+4\right|+5\le5\forall x\)
Dấu '=' xảy ra khi x=-4
Bài 3:
b) Xét số \(-B_3=6+\left|x+4\right|\ge6\Rightarrow B_3\le-6\)
Dấu '=' xảy ra \(\Leftrightarrow x=-4\)

Dựa vào thuật toán sau viết chương trình đó b, xin lỗi mình kh ghi rõ
a, Xét tam giá GHK và tam giác KIG có
GH = IK ( gt)
góc HGK = góc GKI(gt)
GK chung
=> tam giác GHK = tam giác KIG ( c-g-c)
=> GI = HK
=> góc IGK = góc KHG
Ta có góc IGK = góc KHG
=> GI //HK