I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)

\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:

\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)

Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt

Phương trình AB:

\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)

B là giao điểm AB và BC nên tọa độ là nghiệm:

\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)

I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)

AN chính là đường thẳng AB nên AB: x-2y-2=0.

AD qua M(3/2;-3/2) và vuông góc với AB nên AD: 2x+y-3/2=0. Suy ra A(1;-1/2)

Vì M là trung điểm AD nên D(2;-5/2) suy ra BC=AD=\(\sqrt{5}\), suy ra AB=3BC=3\(\sqrt{5}\)

B(2b+2;b) nên 

\(AB=\sqrt{(2b+1)^2+(b+1/2)^2}=\dfrac{\sqrt{5}}{2}|2b+1|=3\sqrt{5}\Rightarrow b=\dfrac{5}{2}\) hoặc \(b=-\dfrac{7}{2}\)

Nếu \(b=\dfrac{5}{2}\) thì B(7;5/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(8;-1/2) (thỏa mãn)

Nếu \(b=-\dfrac{7}{2}\) thì B(-5;-7/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(-4;-11/2) (loại)

lạy mẹ mẹ hok cấp  3 chưa v~

Đặt BC=a, suy ra AB=3a.

$S_{MNC}=S_{ABCD}-S_{AMN}-S_{BNC}-S_{DMC}=3a^2-\dfrac{a^2}{4}-a^2-\dfrac{3a^2}{4}=a^2$

$CN=a\sqrt{5}$ nên $d(M,CN)=\dfrac{2S_{MNC}}{CN}=\dfrac{2a}{\sqrt{5}}$

Mặt khác $d(M,CN)=\dfrac{4}{\sqrt{10}}$ nên $a=\sqrt{2}$

Suy ra $MC=\dfrac{a\sqrt{37}a}{2}=\dfrac{\sqrt{74}}{2}$

Gọi C(3c+2;c) (3c+2>0) thì

$MC^2=(3c+1/2)^2+(c+3/2)^2=\dfrac{74}{4}\Leftrightarrow (6c+1)^2+(2c+3)^2=74$

$40c^2+24c-64=0$ nên c=1 hoặc c=-8/5(loại) nên C(5;1)

+ Tương tự tìm được N từ việc N thuộc CN, $MN=\dfrac{a\sqrt{5}}{2},CN=a\sqrt{5}$

+ Sau khi tìm được N ta tìm được E từ việc M là trung điểm CE

+ Tọa độ A, B xác định qua hệ thức véc tơ: vecto(EA)=3.vecto(AN); vecto(AN)=2vecto(NB)

+ Tọa độ D xác định từ việc M là trung điểm AD.

Đáp án A

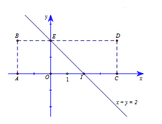
Để con châu chấu đáp xuống các điểm M x , y  có x + y < 2  thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA

Để M x , y có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 , y ∈ 0 ; 1 ; 2  

Nếu x ∈ − 2 ; − 1 thì y ∈ 0 ; 1 ; 2 ⇒ có 2.3 = 6 điểm

Nếu x = 0  thì y ∈ 0 ; 1 ⇒  có 2 điểm

Nếu  x = 1 ⇒ y = 0 ⇒ có 1 điểm

 có tất cả 6 + 2 + 1 = 9  điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ − 2 ; − 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ 0 ; 1 ; 2 ⇒

Số các điểm M x , y  có tọa độ nguyên là: 7.3 = 21  điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

Đáp án A

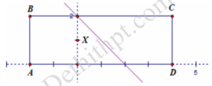
Đường thẳng x + y − 2 = 0 chia hình chữ nhật thành 2 phần như hình vẽ. Xét điểm X 0 ; 1  

Số các điểm nguyên không nằm bên ngoài hình chữ nhật là 3.7 = 21  (điểm)

Các điểm có tọa độ thỏa mãn x + y < 2  là các điểm nằm phía bên trái đường thẳng x + y − 2 = 0 , hay cùng phía với X so với đường thẳng x + y − 2 = 0  và không lấy các điểm nằm trên đường thẳng này.

Dễ thấy trường hợp này có 9 điểm thỏa mãn

Vậy xác suất cần tìm là 9 21 = 3 7

Gọi \(C\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-6;2\right)\\\overrightarrow{BC}=\left(x+2;-4\right)\end{matrix}\right.\)

Tam giác ABC vuông tại B \(\Leftrightarrow\overrightarrow{AB}.\overrightarrow{BC}=0\)

\(\Rightarrow-6\left(x+2\right)-8=0\) \(\Rightarrow x=-\dfrac{10}{3}\)

\(\Rightarrow C\left(-\dfrac{10}{3};0\right)\)

Bạn tự tính tọa độ \(\overrightarrow{AC};\overrightarrow{BC}\) từ đó suy ra độ dài 3 cạnh và tính được chu vi, diện tích

Do tam giác ABC vuông tại B nên ABCD là hcn khi \(\overrightarrow{AB}=\overrightarrow{DC}\)

Gọi \(D\left(x;y\right)\Rightarrow\overrightarrow{DC}=\left(-\dfrac{10}{3}-x;-y\right)\)

\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{10}{3}-x=-6\\-y=2\end{matrix}\right.\) \(\Rightarrow D\left(\dfrac{8}{3};-2\right)\)

Chọn C

Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì

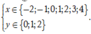
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2

thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA

Để M(x,y) có tọa độ nguyên thì

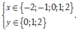
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2

⇒ có 6 điểm

= Nếu x = 0 thì  y ∈ 0 ; 1 ⇒  có 2 điểm

= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm

⇒  có tất cả 6 + 2 +1 = 9 điểm thỏa mãn

Vậy xác suất cần tính  P = 9 21 = 3 7

Hình chữ nhật ADN gì bạn nhỉ?

Hình chữ nhật phải có 4 đỉnh